 Boost
C++ Libraries
Boost
C++ Libraries
...one of the most highly
regarded and expertly designed C++ library projects in the
world.
— Herb Sutter and Andrei
Alexandrescu, C++
Coding Standards
 Boost
C++ Libraries
Boost
C++ Libraries
...one of the most highly
regarded and expertly designed C++ library projects in the
world.
— Herb Sutter and Andrei
Alexandrescu, C++
Coding Standards
The exponential funtion is defined, for all object for which this makes sense,
as the power series 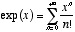 , with
, with n! = 1x2x3x4x5...xn
(and 0! = 1 by definition) being
the factorial of n. In particular,
the exponential function is well defined for real numbers, complex number,
quaternions, octonions, and matrices of complex numbers, among others.
Graph of exp on R
Real and Imaginary parts of exp on C
The hyperbolic functions are defined as power series which can be computed (for reals, complex, quaternions and octonions) as:
Hyperbolic cosine: 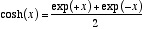
Hyperbolic sine: 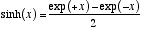
Hyperbolic tangent: 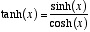
Trigonometric functions on R (cos: purple; sin: red; tan: blue)
Hyperbolic functions on r (cosh: purple; sinh: red; tanh: blue)
The hyperbolic sine is one to one on the set of real numbers, with range
the full set of reals, while the hyperbolic tangent is also one to one on
the set of real numbers but with range ]-1;1[, and therefore
both have inverses. The hyperbolic cosine is one to one from [0;+
∞
[ onto [+1;+
∞
[ (and from ]-
∞
;0] onto [+1;+
∞
[); the inverse function we use here is defined on [+1;+
∞
[ with range [0;+
∞
[.
The inverse of the hyperbolic tangent is called the Argument hyperbolic tangent,
and can be computed as 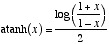 .
.
The inverse of the hyperbolic sine is called the Argument hyperbolic sine,
and can be computed (for x
≥
0) as 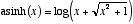 .
.
The inverse of the hyperbolic cosine is called the Argument hyperbolic cosine,
and can be computed as 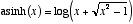 .
.
The Sinus Cardinal family of functions (indexed by the family of indices
a > 0) is defined by 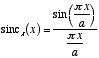 ; it sees heavy use in signal processing tasks.
; it sees heavy use in signal processing tasks.
By analogy, the Hyperbolic Sinus Cardinal family of functions (also indexed
by the family of indices a > 0) is defined by 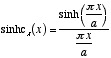 .
.
These two families of functions are composed of entire functions.
Sinus Cardinal of index pi (purple) and Hyperbolic Sinus Cardinal of index pi (red) on R
Please refer to the following PDF's:
| Copyright © 2001 -2002 Daryle Walker, 2001-2003 Hubert Holin, 2005 John Maddock |