 Boost
C++ Libraries
Boost
C++ Libraries
...one of the most highly
regarded and expertly designed C++ library projects in the
world.
— Herb Sutter and Andrei
Alexandrescu, C++
Coding Standards
 Boost
C++ Libraries
Boost
C++ Libraries
...one of the most highly
regarded and expertly designed C++ library projects in the
world.
— Herb Sutter and Andrei
Alexandrescu, C++
Coding Standards
The Special Functions library currently provides eight templated special functions, in namespace boost. Two of these (sinc_pi and sinhc_pi) are needed by our implementation of quaternions and octonions.
The functions acosh, asinh and atanh are entirely classical, the function sinc_pi sees heavy use in signal processing tasks, and the function sinhc_pi is an ad'hoc function whose naming is modelled on sinc_pi and hyperbolic functions.
The functions log1p, expm1 and hypot are all part of the C99 standard but not yet C++. Two of these (log1p and hypot) were needed for the complex number inverse trigonometric functions.
The functions implemented here can throw standard exceptions, but no exception specification has been made.
The interface and implementation for each function (or forms of a function) are both supplied by one header file:
namespace boost{ namespace math{ template<typename T> T acosh(const T x); template<typename T> T asinh(const T x); template<typename T> T atanh(const T x); template<typename T> T expm1(const T x); template<typename T> T hypot(const T x); template<typename T> T log1p(const T x); template<typename T> T sinc_pi(const T x); template<typename T, template<typename> class U> U<T> sinc_pi(const U<T> x); template<typename T> T sinhc_pi(const T x); template<typename T, template<typename> class U> U<T> sinhc_pi(const U<T> x); } }
template<typename T> T acosh(const T x);
Computes the reciprocal of (the restriction to the range of [0;+
∞
[) the
hyperbolic cosine function, at x. Values returned are positive. Generalised
Taylor series are used near 1 and Laurent series are used near the infinity
to ensure accuracy.
If x is in the range ]-
∞
;+1[ a quiet NaN is returned (if the system allows, otherwise a
domain_error exception is
generated).
template<typename T> T asinh(const T x);
Computes the reciprocal of the hyperbolic sine function. Taylor series are used at the origin and Laurent series are used near the infinity to ensure accuracy.
template<typename T> T atanh(const T x);
Computes the reciprocal of the hyperbolic tangent function, at x. Taylor series are used at the origin to ensure accuracy.
If x is in the range ]-
∞
;-1[ or in the range ]+1;+
∞
[ a quiet NaN is returned (if the system allows, otherwise a domain_error exception is generated).
If x is in the range `[-1;-1+
ε
[, minus infinity is returned (if the system allows, otherwise
an out_of_range exception
is generated), with
ε
denoting numeric_limits<T>::epsilon().
If x is in the range ]+1-
ε
;+1], plus infinity is returned (if the system allows, otherwise
an out_of_range exception
is generated), with
ε
denoting numeric_limits<T>::epsilon().
template <class T> T expm1(T t);
Effects: returns
ex - 1
.
For small x, then
ex
is very close to 1, as a result calculating
ex - 1
results in catastrophic cancellation errors when x is small. expm1 calculates
ex - 1
using a series expansion when x is small (giving an accuracy of less than
2ε
).
Finally when BOOST_HAS_EXPM1 is defined then the float/double/long double
specializations of this template simply forward to the platform's native
implementation of this function.
template <class T> T hypot(T x, T y);
Effects: computes 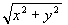 in such a way as to avoid undue underflow and overflow.
in such a way as to avoid undue underflow and overflow.
When calculating 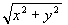 it's quite easy for the intermediate terms to either
overflow or underflow, even though the result is in fact perfectly representable.
One possible alternative form is
it's quite easy for the intermediate terms to either
overflow or underflow, even though the result is in fact perfectly representable.
One possible alternative form is 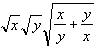 , but that can overflow or underflow if x and y are of
very differing magnitudes. The
, but that can overflow or underflow if x and y are of
very differing magnitudes. The hypot
function takes care of all the special cases for you, so you don't have to.
template <class T> T log1p(T x);
Effects: returns the natural logarithm
of x+1.
There are many situations where it is desirable to compute log(x+1).
However, for small x then
x+1 suffers from catastrophic cancellation errors
so that x+1 == 1 and log(x+1) == 0, when in fact for very small x, the best
approximation to log(x+1) would be x.
log1p calculates the best
approximation to log(1+x) using a Taylor series expansion for accuracy
(less than
2ε
). Note that there are faster methods available, for example using the equivalence:
log(1+x) == (log(1+x) * x) / ((1-x) - 1)
However, experience has shown that these methods tend to fail quite spectacularly once the compiler's optimizations are turned on. In contrast, the series expansion method seems to be reasonably immune optimizer-induced errors.
Finally when BOOST_HAS_LOG1P is defined then the float/double/long double
specializations of this template simply forward to the platform's native
implementation of this function.
template<typename T> T sinc_pi(const T x); template<typename T, template<typename> class U> U<T> sinc_pi(const U<T> x);
Computes the Sinus Cardinal of x. The second form is for complexes, quaternions, octonions... Taylor series are used at the origin to ensure accuracy.
template<typename T> T sinhc_pi(const T x); template<typename T, template<typename> class U> U<T> sinhc_pi(const U<T> x);
Computes the Hyperbolic Sinus Cardinal of x. The second form is for complexes, quaternions, octonions... Taylor series are used at the origin to ensure accuracy.
The special_functions_test.cpp and log1p_expm1_test.cpp test programs test the functions for float, double and long double arguments (sample output, with message output enabled).
If you define the symbol BOOST_SPECIAL_FUNCTIONS_TEST_VERBOSE, you will get
additional output (verbose
output), which may prove useful for tuning on your platform (the
library use "reasonable" tolerances, which may prove to be too
strict for your platform); this will only be helpfull if you enable message
output at the same time, of course (by uncommenting the relevant line in
the test or by adding --log_level=messages
to your command line,...).
The mathematical text has been typeset with Nisus Writer, and the illustrations have been made with Graphing Calculator. Jens Maurer was the Review Manager for this library. More acknowledgements in the History section. Thank you to all who contributed to the discution about this library.
| Copyright © 2001 -2002 Daryle Walker, 2001-2003 Hubert Holin, 2005 John Maddock |