 Boost
C++ Libraries
Boost
C++ Libraries
...one of the most highly
regarded and expertly designed C++ library projects in the
world.
— Herb Sutter and Andrei
Alexandrescu, C++
Coding Standards
 Boost
C++ Libraries
Boost
C++ Libraries
...one of the most highly
regarded and expertly designed C++ library projects in the
world.
— Herb Sutter and Andrei
Alexandrescu, C++
Coding Standards
#include <boost/math/special_functions/beta.hpp>
namespace boost{ namespace math{ template <class T1, class T2> calculated-result-type beta(T1 a, T2 b); template <class T1, class T2, class Policy> calculated-result-type beta(T1 a, T2 b, const Policy&); }} // namespaces
The beta function is defined by:

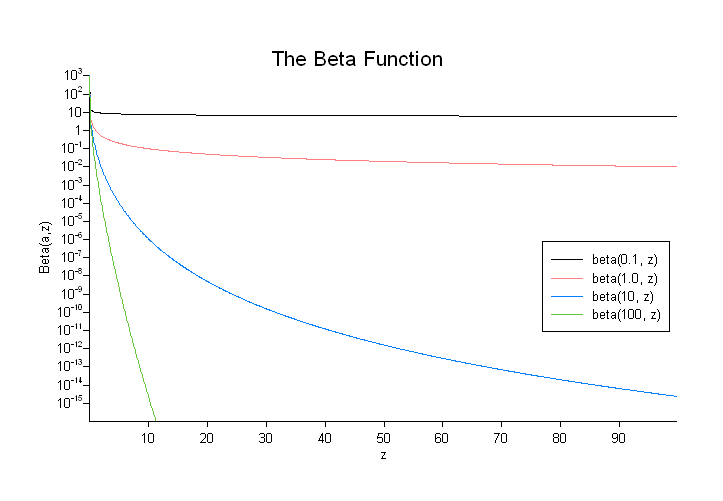
The final Policy argument is optional and can be used to control the behaviour of the function: how it handles errors, what level of precision to use etc. Refer to the policy documentation for more details.
There are effectively two versions of this function internally: a fully generic version that is slow, but reasonably accurate, and a much more efficient approximation that is used where the number of digits in the significand of T correspond to a certain Lanczos approximation. In practice any built-in floating-point type you will encounter has an appropriate Lanczos approximation defined for it. It is also possible, given enough machine time, to generate further Lanczos approximation's using the program libs/math/tools/lanczos_generator.cpp.
The return type of these functions is computed using the result type calculation rules when T1 and T2 are different types.
The following table shows peak errors for various domains of input arguments, along with comparisons to the GSL-1.9 and Cephes libraries. Note that only results for the widest floating point type on the system are given as narrower types have effectively zero error.
Table 17. Peak Errors In the Beta Function
|
Significand Size |
Platform and Compiler |
Errors in range 0.4 < a,b < 100 |
Errors in range 1e-6 < a,b < 36 |
|---|---|---|---|
|
53 |
Win32, Visual C++ 8 |
Peak=99 Mean=22 (GSL Peak=1178 Mean=238) (Cephes=1612) |
Peak=10.7 Mean=2.6 (GSL Peak=12 Mean=2.0) (Cephes=174) |
|
64 |
Red Hat Linux IA32, g++ 3.4.4 |
Peak=112.1 Mean=26.9 |
Peak=15.8 Mean=3.6 |
|
64 |
Red Hat Linux IA64, g++ 3.4.4 |
Peak=61.4 Mean=19.5 |
Peak=12.2 Mean=3.6 |
|
113 |
HPUX IA64, aCC A.06.06 |
Peak=42.03 Mean=13.94 |
Peak=9.8 Mean=3.1 |
Note that the worst errors occur when a or b are large, and that when this is the case the result is very close to zero, so absolute errors will be very small.
A mixture of spot tests of exact values, and randomly generated test data are used: the test data was computed using NTL::RR at 1000-bit precision.
Traditional methods of evaluating the beta function either involve evaluating the gamma functions directly, or taking logarithms and then exponentiating the result. However, the former is prone to overflows for even very modest arguments, while the latter is prone to cancellation errors. As an alternative, if we regard the gamma function as a white-box containing the Lanczos approximation, then we can combine the power terms:
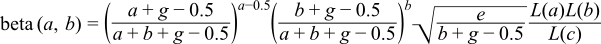
which is almost the ideal solution, however almost all of the error occurs in evaluating the power terms when a or b are large. If we assume that a > b then the larger of the two power terms can be reduced by a factor of b, which immediately cuts the maximum error in half:
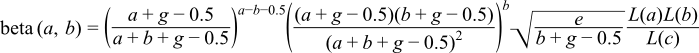
This may not be the final solution, but it is very competitive compared to other implementation methods.
The generic implementation - where no Lanczos approximation approximation is available - is implemented in a very similar way to the generic version of the gamma function. Again in order to avoid numerical overflow the power terms that prefix the series and continued fraction parts are collected together into:

where la, lb and lc are the integration limits used for a, b, and a+b.
There are a few special cases worth mentioning:
When a or b are less than one, we can use the recurrence relations:


to move to a more favorable region where they are both greater than 1.
In addition:
