 Boost
C++ Libraries
Boost
C++ Libraries
...one of the most highly
regarded and expertly designed C++ library projects in the
world.
— Herb Sutter and Andrei
Alexandrescu, C++
Coding Standards
 Boost
C++ Libraries
Boost
C++ Libraries
...one of the most highly
regarded and expertly designed C++ library projects in the
world.
— Herb Sutter and Andrei
Alexandrescu, C++
Coding Standards
boost::accumulators::impl::weighted_kurtosis_impl — Kurtosis estimation for weighted samples.
template<typename Sample, typename Weight> struct weighted_kurtosis_impl { // types typedef numeric::functional::multiplies< Sample, Weight >::result_type weighted_sample; typedef numeric::functional::average< weighted_sample, weighted_sample >::result_type result_type; // construct/copy/destruct weighted_kurtosis_impl(dont_care); // public member functions template<typename Args> result_type result(Args const &) const; };
The kurtosis of a sample distribution is defined as the ratio of the 4th central moment and the square of the 2nd central moment (the variance) of the samples, minus 3. The term  is added in order to ensure that the normal distribution has zero kurtosis. The kurtosis can also be expressed by the simple moments:
is added in order to ensure that the normal distribution has zero kurtosis. The kurtosis can also be expressed by the simple moments:
where  are the
are the 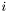 -th moment and
-th moment and 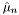 the mean (first moment) of the
the mean (first moment) of the  samples.
samples.
The kurtosis estimator for weighted samples is formally identical to the estimator for unweighted samples, except that the weighted counterparts of all measures it depends on are to be taken.