 Boost
C++ Libraries
Boost
C++ Libraries
...one of the most highly
regarded and expertly designed C++ library projects in the
world.
— Herb Sutter and Andrei
Alexandrescu, C++
Coding Standards
 Boost
C++ Libraries
Boost
C++ Libraries
...one of the most highly
regarded and expertly designed C++ library projects in the
world.
— Herb Sutter and Andrei
Alexandrescu, C++
Coding Standards

template <typename TGraph,
typename TVertexIndexMap,
typename TWeight1EdgeMap,
typename TWeight2EdgeMap >
double maximum_cycle_ratio(const TGraph& g, TVertexIndexMap vim, TWeight1EdgeMap ewm, TWeight2EdgeMap ew2m,
typename std::vector<typename boost::graph_traits<TGraph>::edge_descriptor>* pcc = 0,
typename boost::property_traits<TWeight1EdgeMap>::value_type minus_infinity =
-(std::numeric_limits<int>::max)());
template <typename TGraph,
typename TVertexIndexMap,
typename TWeight1EdgeMap,
typename TWeight2EdgeMap,
typename TEdgeIndexMap >
double minimum_cycle_ratio(const TGraph& g, TVertexIndexMap vim, TWeight1EdgeMap ewm, TWeight2EdgeMap ew2m, TEdgeIndexMap eim,
typename std::vector<typename boost::graph_traits<TGraph>::edge_descriptor>* pcc = 0,
typename boost::property_traits<TWeight1EdgeMap>::value_type plus_infinity =
(std::numeric_limits<int>::max)());
The maximum_cycle_ratio() function calculates the maximum cycle ratio of a weighted directed multigraph g=(V,E,W1,W2), where V is a vertex set, E is an edge set, W1 and W2 are edge weight functions, W2 is nonnegative. Multigraph is a graph that can have multiple edges between its vertices. The calculated maximum cycle ratio will be the return value of the function. The maximal_cycle_ratio() returns minus_infinity if graph has no cycles. The value of the minus_infinity parameter should be small enough to garanty that g has at leat one cycle with greater ratio.
Let every edge e have two weights W1(e) and W2(e). Let c be a cycle of a graph g. The cycle ratio (cr(c)) is defined as:
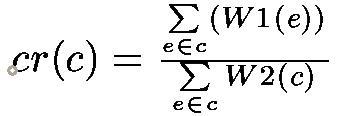
The maximum (minimum) cycle ratio (mcr) is the maximum (minimum) cycle ratio of all cycles of the graph.
Cycle calls critical if its ratio is equal to mcr.
The algorithm is due to Howard's iteration policy algorithm, descibed in [1]. Ali Dasdan, Sandy S. Irani and Rajesh K.Gupta in their paper Efficient Algorithms for Optimum Cycle Mean and Optimum Cost to Time Ratio Problemsstate that this is the most efficient algorithm to the time being (1999).
boost/graph/howard_cycle_ratio.hpp
IN: const TGraph& g
A directed weighted multigraph. The graph's type must be a model of VertexListGraph and IncidenceGraph
IN: TVertexIndexMap vim
Maps each vertex of the graph to a unique integer in the range [0, num_vertices(g)).
IN: TWeight1EdgeMap ew1m
The W1 edge weight function. For minimum_cycle_ratio() if the type value of the ew1m is integral then it must be signed.
IN: TWeight2EdgeMap ew2m
The W2 edge weight function. Must be nonnegative.
IN: TEdgeIndexMap eim
Maps each edge of the graph g to a unique integer in the range [0, num_edges(g)).
IN: boost::property_traits<TWeight1EdgeMap>::value_type minus_infinity
Small enough value to garanty that g has at least one cycle with greater ratio
IN: boost::property_traits<TWeight1EdgeMap>::value_type plus_infinity
Big enough value to garanty that g has at least one cycle with less ratio. Expression -plus_infinity must be well defined.
OUT: std::vector<typename boost::graph_traits<TGraph>::edge_descriptor>* pcc
An edge descriptors of one critical cycle will be stored in the corresponding std::vector. Default value is 0.
The all maps must be a models of Readable Property Map
There is no known precise upper bound for the time complexity of the algorithm. Imperical time complexity is O(E), where the constant tends to be pretty small. Space complexity is also O(E).
The program in cycle_ratio_example.cpp generates random graph and computes its maximum cycle ratio.
|
Copyright © 2000-2006 |
Dmitry Bufistov, Universitat Politecnica de Cataluña |