 Boost
C++ Libraries
Boost
C++ Libraries
...one of the most highly
regarded and expertly designed C++ library projects in the
world.
— Herb Sutter and Andrei
Alexandrescu, C++
Coding Standards
 Boost
C++ Libraries
Boost
C++ Libraries
...one of the most highly
regarded and expertly designed C++ library projects in the
world.
— Herb Sutter and Andrei
Alexandrescu, C++
Coding Standards
#include <boost/math/special_functions/expint.hpp>
namespace boost{ namespace math{ template <class T> calculated-result-type expint(unsigned n, T z); template <class T, class Policy> calculated-result-type expint(unsigned n, T z, const Policy&); }} // namespaces
The return type of these functions is computed using the result
type calculation rules: the return type is double if T is an integer type, and T otherwise.
The final Policy argument is optional and can be used to control the behaviour of the function: how it handles errors, what level of precision to use etc. Refer to the policy documentation for more details.
template <class T> calculated-result-type expint(unsigned n, T z); template <class T, class Policy> calculated-result-type expint(unsigned n, T z, const Policy&);
Returns the exponential integral En of z:


The following table shows the peak errors (in units of epsilon) found on various platforms with various floating point types, along with comparisons to the Cephes library. Unless otherwise specified any floating point type that is narrower than the one shown will have effectively zero error.
Table 45. Errors In the Function expint(n, z)
|
Significand Size |
Platform and Compiler |
En |
E1 |
|---|---|---|---|
|
53 |
Win32, Visual C++ 8 |
Peak=7.1 Mean=1.8 Cephes Peak=5.1 Mean=1.3 |
Peak=0.99 Mean=0.5 Cephes Peak=3.1 Mean=1.1 |
|
64 |
RedHat Linux IA_EM64, gcc-4.1 |
Peak=9.9 Mean=2.1 |
Peak=0.97 Mean=0.4 |
|
64 |
Redhat Linux IA64, gcc-4.1 |
Peak=9.9 Mean=2.1 |
Peak=0.97 Mean=0.4 |
|
113 |
HPUX IA64, aCC A.06.06 |
Peak=23.3 Mean=3.7 |
Peak=1.6 Mean=0.5 |
The tests for these functions come in two parts: basic sanity checks use spot values calculated using Mathworld's online evaluator, while accuracy checks use high-precision test values calculated at 1000-bit precision with NTL::RR and this implementation. Note that the generic and type-specific versions of these functions use differing implementations internally, so this gives us reasonably independent test data. Using our test data to test other "known good" implementations also provides an additional sanity check.
The generic version of this function uses the continued fraction:

for large x and the infinite series:

for small x.
Where the precision of x is known at compile time
and is 113 bits or fewer in precision, then rational approximations devised
by JM are used for the n
== 1
case.
For x <
1 the approximating form is a minimax
approximation:

and for x >
1 a Chebyshev interpolated approximation
of the form:
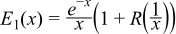
is used.