 Boost
C++ Libraries
Boost
C++ Libraries
...one of the most highly
regarded and expertly designed C++ library projects in the
world.
— Herb Sutter and Andrei
Alexandrescu, C++
Coding Standards
 Boost
C++ Libraries
Boost
C++ Libraries
...one of the most highly
regarded and expertly designed C++ library projects in the
world.
— Herb Sutter and Andrei
Alexandrescu, C++
Coding Standards
 Breadth-First Search
Breadth-First Search
// named parameter version
template <class Graph, class P, class T, class R>
void breadth_first_search(Graph& G,
typename graph_traits<Graph>::vertex_descriptor s,
const bgl_named_params<P, T, R>& params);
// non-named parameter version
template <class Graph, class Buffer, class BFSVisitor,
class ColorMap>
void breadth_first_search(const Graph& g,
typename graph_traits<Graph>::vertex_descriptor s,
Buffer& Q, BFSVisitor vis, ColorMap color);
The breadth_first_search() function performs a distributed breadth-first traversal of a directed or undirected graph. The distributed BFS is syntactically equivalent to its sequential counterpart, which provides additional background and discussion. Differences in semantics are highlighted here, and we refer the reader to the documentation of the sequential breadth-first search for the remainder of the details.
This distributed breadth-first search algorithm implements a level-synchronized breadth-first search, meaning that all vertices in a given level of the BFS tree will be processed (potentially in parallel) before any vertices from a successive level in the tree are processed. Distributed breadth-first search visitors should account for this behavior, a topic discussed further in Visitor Event Points.
Contents
<boost/graph/breadth_first_search.hpp>
All parameters of the sequential breadth-first search are supported and have essentially the same meaning. Only differences are documented here.
The queue must be a distributed queue that passes vertices to their owning process. If already-visited vertices should not be visited again (as is typical for BFS), the queue must filter duplicates itself. The queue controls synchronization within the algorithm: its empty() method must not return true until all local queues are empty.
This algorithm performs O(V + E) work in d + 1 BSP supersteps, where d is the diameter of the connected component being searched. Over all supersteps, O(E) messages of constant size will be transmitted.
The BFS Visitor concept defines 9 event points that will be triggered by the sequential breadth-first search. The distributed BFS retains these nine event points, but the sequence of events triggered and the process in which each event occurs will change depending on the distribution of the graph.
The three most important things to remember when updating an existing BFS visitor for distributed BFS or writing a new distributed BFS visitor are:
To illustrate the differences between sequential and distributed BFS visitors, we consider a BFS visitor that places the distance from the source vertex to every other vertex in a property map. The sequential visitor is very simple:
template<typename DistanceMap>
struct bfs_discovery_visitor : bfs_visitor<>
{
bfs_discovery_visitor(DistanceMap distance) : distance(distance) {}
template<typename Edge, typename Graph>
void tree_edge(Edge e, const Graph& g)
{
std::size_t new_distance = get(distance, source(e, g)) + 1;
put(distance, target(e, g), new_distance);
}
private:
DistanceMap distance;
};
To revisit this code for distributed BFS, we consider the three points in the section Making Visitors Safe for Distributed BFS:
The distance map will need to become distributed, because the distance to each vertex should be stored in the process owning the vertex. This is actually a requirement on the user to provide such a distributed property map, although in many cases the property map will automatically be distributed and no syntactic changes will be required.
This visitor does require a precise sequence of events that may change with a distributed BFS. The extraneous tree_edge events that may occur could result in attempts to put distances into the distance map multiple times for a single vertex. We therefore need to consider bullet #3.
Since multiple distance values may be written for each vertex, we must always choose the best value we can find to update the distance map. The distributed property map distance needs to resolve distances to the smallest distance it has seen. For instance, process 0 may find vertex u at level 3 but process 1 finds it at level 5: the distance must remain at 3. To do this, we state that the property map's role is as a distance map, which introduces an appropriate reduction operation:
set_property_map_role(vertex_distance, distance);
The resulting distributed BFS visitor (which also applies, with no changes, in the sequential BFS) is very similar to our original sequential BFS visitor. Note the single-line difference in the constructor:
template<typename DistanceMap>
struct bfs_discovery_visitor : bfs_visitor<>
{
bfs_discovery_visitor(DistanceMap distance) : distance(distance)
{
set_property_map_role(vertex_distance, distance);
}
template<typename Edge, typename Graph>
void tree_edge(Edge e, const Graph& g)
{
std::size_t new_distance = get(distance, source(e, g)) + 1;
put(distance, target(e, g), new_distance);
}
private:
DistanceMap distance;
};
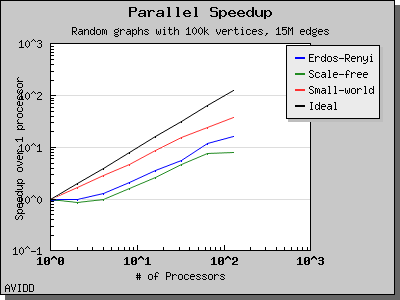
The performance of Breadth-First Search is illustrated by the following charts. Scaling and performance is reasonable for all of the graphs we have tried.
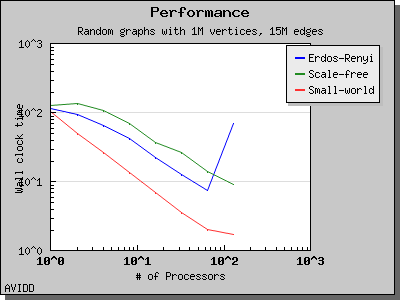
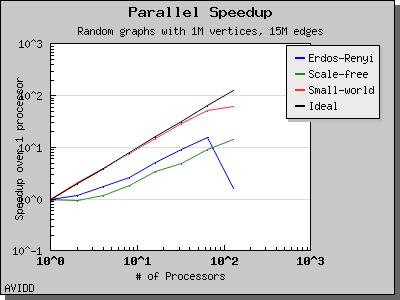
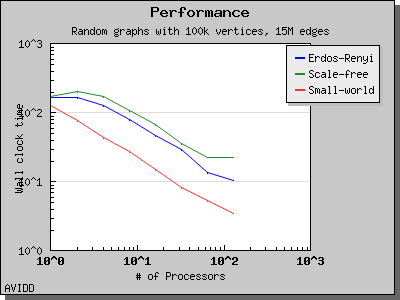
Copyright (C) 2004 The Trustees of Indiana University.
Authors: Douglas Gregor and Andrew Lumsdaine