 Boost
C++ Libraries
Boost
C++ Libraries
...one of the most highly
regarded and expertly designed C++ library projects in the
world.
— Herb Sutter and Andrei
Alexandrescu, C++
Coding Standards
 Boost
C++ Libraries
Boost
C++ Libraries
...one of the most highly
regarded and expertly designed C++ library projects in the
world.
— Herb Sutter and Andrei
Alexandrescu, C++
Coding Standards
#include <boost/math/tools/roots.hpp>
namespace boost{ namespace math{ namespace tools{ template <class F, class T> T newton_raphson_iterate(F f, T guess, T min, T max, int digits); template <class F, class T> T newton_raphson_iterate(F f, T guess, T min, T max, int digits, boost::uintmax_t& max_iter); template <class F, class T> T halley_iterate(F f, T guess, T min, T max, int digits); template <class F, class T> T halley_iterate(F f, T guess, T min, T max, int digits, boost::uintmax_t& max_iter); template <class F, class T> T schroeder_iterate(F f, T guess, T min, T max, int digits); template <class F, class T> T schroeder_iterate(F f, T guess, T min, T max, int digits, boost::uintmax_t& max_iter); }}} // namespaces
These functions all perform iterative root finding: newton_raphson_iterate
performs second order Newton Raphson iteration,
while halley_iterate and
schroeder_iterate perform
third order Halley and Schroeder
iteration respectively.
The functions all take the same parameters:
Parameters of the root finding functions
Type F must be a callable function object that accepts one parameter and returns a boost::math::tuple:
For the second order iterative methods (Newton Raphson) the boost::math::tuple should have two elements containing the evaluation of the function and it's first derivative.
For the third order methods (Halley and Schroeder) the boost::math::tuple should have three elements containing the evaluation of the function and its first and second derivatives.
The initial starting value.
The minimum possible value for the result, this is used as an initial lower bracket.
The maximum possible value for the result, this is used as an initial upper bracket.
The desired number of binary digits.
An optional maximum number of iterations to perform.
When using these functions you should note that:
Given an initial guess x0 the subsequent values are computed using:

Out of bounds steps revert to bisection of the current bounds.
Under ideal conditions, the number of correct digits doubles with each iteration.
Given an initial guess x0 the subsequent values are computed using:

Over-compensation by the second derivative (one which would proceed in the wrong direction) causes the method to revert to a Newton-Raphson step.
Out of bounds steps revert to bisection of the current bounds.
Under ideal conditions, the number of correct digits trebles with each iteration.
Given an initial guess x0 the subsequent values are computed using:
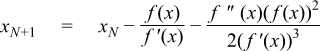
Over-compensation by the second derivative (one which would proceed in the wrong direction) causes the method to revert to a Newton-Raphson step. Likewise a Newton step is used whenever that Newton step would change the next value by more than 10%.
Out of bounds steps revert to bisection of the current bounds.
Under ideal conditions, the number of correct digits trebles with each iteration.
Lets suppose we want to find the cube root of a number, the equation we want to solve along with its derivatives are:

To begin with lets solve the problem using Newton Raphson iterations, we'll begin be defining a function object that returns the evaluation of the function to solve, along with its first derivative:
template <class T> struct cbrt_functor { cbrt_functor(T const& target) : a(target){} boost::math::tuple<T, T> operator()(T const& z) { T sqr = z * z; return std::tr1::make_tuple(sqr * z - a, 3 * sqr); } private: T a; };
Implementing the cube root is fairly trivial now, the hardest part is finding a good approximation to begin with: in this case we'll just divide the exponent by three:
template <class T> T cbrt(T z) { using namespace std; int exp; frexp(z, &exp); T min = ldexp(0.5, exp/3); T max = ldexp(2.0, exp/3); T guess = ldexp(1.0, exp/3); int digits = std::numeric_limits<T>::digits; return tools::newton_raphson_iterate(detail::cbrt_functor<T>(z), guess, min, max, digits); }
Using the test data in libs/math/test/cbrt_test.cpp this found the cube
root exact to the last digit in every case, and in no more than 6 iterations
at double precision. However, you will note that a high precision was used
in this example, exactly what was warned against earlier on in these docs!
In this particular case its possible to compute f(x) exactly and without
undue cancellation error, so a high limit is not too much of an issue.
However, reducing the limit to std::numeric_limits<T>::digits
* 2 / 3 gave
full precision in all but one of the test cases (and that one was out by
just one bit). The maximum number of iterations remained 6, but in most
cases was reduced by one.
Note also that the above code omits error handling, and does not handle negative values of z correctly. That will be left as an exercise for the reader!
Now lets adapt the functor slightly to return the second derivative as well:
template <class T> struct cbrt_functor { cbrt_functor(T const& target) : a(target){} boost::math::tuple<T, T, T> operator()(T const& z) { T sqr = z * z; return std::tr1::make_tuple(sqr * z - a, 3 * sqr, 6 * z); } private: T a; };
And then adapt the cbrt
function to use Halley iterations:
template <class T> T cbrt(T z) { using namespace std; int exp; frexp(z, &exp); T min = ldexp(0.5, exp/3); T max = ldexp(2.0, exp/3); T guess = ldexp(1.0, exp/3); int digits = std::numeric_limits<T>::digits / 2; return tools::halley_iterate(detail::cbrt_functor<T>(z), guess, min, max, digits); }
Note that the iterations are set to stop at just one-half of full precision, and yet even so not one of the test cases had a single bit wrong. What's more, the maximum number of iterations was now just 4.
Just to complete the picture, we could have called schroeder_iterate
in the last example: and in fact it makes no difference to the accuracy
or number of iterations in this particular case. However, the relative
performance of these two methods may vary depending upon the nature of
f(x), and the accuracy to which the initial guess can be computed. There
appear to be no generalisations that can be made except "try them
and see".
Finally, had we called cbrt with NTL::RR set to 1000 bit precision, then full precision can be obtained with just 7 iterations. To put that in perspective an increase in precision by a factor of 20, has less than doubled the number of iterations. That just goes to emphasise that most of the iterations are used up getting the first few digits correct: after that these methods can churn out further digits with remarkable efficiency. Or to put it another way: nothing beats a really good initial guess!