 Boost
C++ Libraries
Boost
C++ Libraries
...one of the most highly
regarded and expertly designed C++ library projects in the
world.
— Herb Sutter and Andrei
Alexandrescu, C++
Coding Standards
 Boost
C++ Libraries
Boost
C++ Libraries
...one of the most highly
regarded and expertly designed C++ library projects in the
world.
— Herb Sutter and Andrei
Alexandrescu, C++
Coding Standards
 Dijkstra's Single-Source Shortest Paths
Dijkstra's Single-Source Shortest Paths
// named parameter version
template <typename Graph, typename P, typename T, typename R>
void
dijkstra_shortest_paths(Graph& g,
typename graph_traits<Graph>::vertex_descriptor s,
const bgl_named_params<P, T, R>& params);
// non-named parameter version
template <typename Graph, typename DijkstraVisitor,
typename PredecessorMap, typename DistanceMap,
typename WeightMap, typename VertexIndexMap, typename CompareFunction, typename CombineFunction,
typename DistInf, typename DistZero>
void dijkstra_shortest_paths
(const Graph& g,
typename graph_traits<Graph>::vertex_descriptor s,
PredecessorMap predecessor, DistanceMap distance, WeightMap weight,
VertexIndexMap index_map,
CompareFunction compare, CombineFunction combine, DistInf inf, DistZero zero,
DijkstraVisitor vis);
The dijkstra_shortest_paths() function solves the single-source shortest paths problem on a weighted, undirected or directed distributed graph. There are two implementations of distributed Dijkstra's algorithm, which offer different performance tradeoffs. Both are accessible via the dijkstra_shortest_paths() function (for compatibility with sequential BGL programs). The distributed Dijkstra algorithms are very similar to their sequential counterparts. Only the differences are highlighted here; please refer to the sequential Dijkstra implementation for additional details. The best-performing implementation for most cases is the Delta-Stepping algorithm; however, one can also employ the more conservative Crauser et al.'s algorithm or the simlistic Eager Dijkstra's algorithm.
Contents
<boost/graph/dijkstra_shortest_paths.hpp>
All parameters of the sequential Dijkstra implementation are supported and have essentially the same meaning. The distributed Dijkstra implementations introduce a new parameter that allows one to select Eager Dijkstra's algorithm and control the amount of work it performs. Only differences and new parameters are documented here.
The predecessor map must be a Distributed Property Map or dummy_property_map, although only the local portions of the map will be written.
Default: dummy_property_map
IN: lookahead(distance_type look)
When this parameter is supplied, the implementation will use the Eager Dijkstra's algorithm with the given lookahead value. Lookahead permits distributed Dijkstra's algorithm to speculatively process vertices whose shortest distance from the source may not have been found yet. When the distance found is the shortest distance, parallelism is improved and the algorithm may terminate more quickly. However, if the distance is not the shortest distance, the vertex will need to be reprocessed later, resulting in more work.
The type distance_type is the value type of the DistanceMap property map. It is a nonnegative value specifying how far ahead Dijkstra's algorithm may process values.
Default: no value (lookahead is not employed; uses Crauser et al.'s algorithm).
The Dijkstra Visitor concept defines 7 event points that will be triggered by the sequential Dijkstra implementation. The distributed Dijkstra retains these event points, but the sequence of events triggered and the process in which each event occurs will change depending on the distribution of the graph, lookahead, and edge weights.
namespace graph {
template<typename DistributedGraph, typename DijkstraVisitor,
typename PredecessorMap, typename DistanceMap, typename WeightMap,
typename IndexMap, typename ColorMap, typename Compare,
typename Combine, typename DistInf, typename DistZero>
void
crauser_et_al_shortest_paths
(const DistributedGraph& g,
typename graph_traits<DistributedGraph>::vertex_descriptor s,
PredecessorMap predecessor, DistanceMap distance, WeightMap weight,
IndexMap index_map, ColorMap color_map,
Compare compare, Combine combine, DistInf inf, DistZero zero,
DijkstraVisitor vis);
template<typename DistributedGraph, typename DijkstraVisitor,
typename PredecessorMap, typename DistanceMap, typename WeightMap>
void
crauser_et_al_shortest_paths
(const DistributedGraph& g,
typename graph_traits<DistributedGraph>::vertex_descriptor s,
PredecessorMap predecessor, DistanceMap distance, WeightMap weight);
template<typename DistributedGraph, typename DijkstraVisitor,
typename PredecessorMap, typename DistanceMap>
void
crauser_et_al_shortest_paths
(const DistributedGraph& g,
typename graph_traits<DistributedGraph>::vertex_descriptor s,
PredecessorMap predecessor, DistanceMap distance);
}
The formulation of Dijkstra's algorithm by Crauser, Mehlhorn, Meyer, and Sanders [CMMS98a] improves the scalability of parallel Dijkstra's algorithm by increasing the number of vertices that can be processed in a given superstep. This algorithm adapts well to various graph types, and is a simple algorithm to use, requiring no additional user input to achieve reasonable performance. The disadvantage of this algorithm is that the implementation is required to manage three priority queues, which creates a large amount of work at each node.
This algorithm is used by default in distributed dijkstra_shortest_paths().
<boost/graph/distributed/crauser_et_al_shortest_paths.hpp>
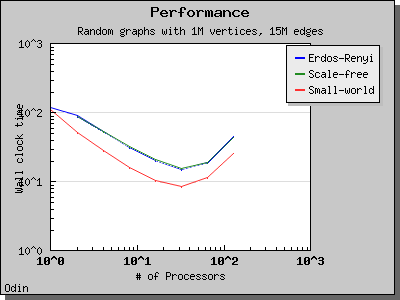
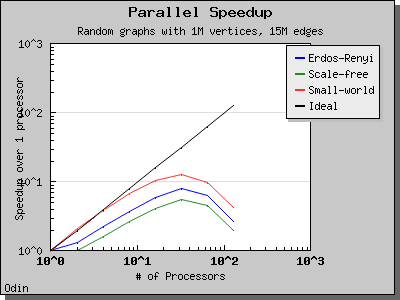
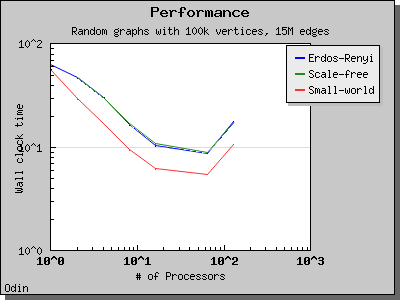
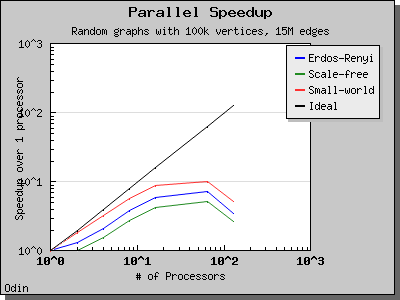
This algorithm performs O(V log V) work in d + 1 BSP supersteps, where d is at most O(V) but is generally much smaller. On directed Erdos-Renyi graphs with edge weights in [0, 1), the expected number of supersteps d is O(n^(1/3)) with high probability.
The following charts illustrate the performance of the Parallel BGL implementation of Crauser et al.'s algorithm on graphs with edge weights uniformly selected from the range [0, 1).
namespace graph {
template<typename DistributedGraph, typename DijkstraVisitor,
typename PredecessorMap, typename DistanceMap, typename WeightMap,
typename IndexMap, typename ColorMap, typename Compare,
typename Combine, typename DistInf, typename DistZero>
void
eager_dijkstra_shortest_paths
(const DistributedGraph& g,
typename graph_traits<DistributedGraph>::vertex_descriptor s,
PredecessorMap predecessor, DistanceMap distance,
typename property_traits<DistanceMap>::value_type lookahead,
WeightMap weight, IndexMap index_map, ColorMap color_map,
Compare compare, Combine combine, DistInf inf, DistZero zero,
DijkstraVisitor vis);
template<typename DistributedGraph, typename DijkstraVisitor,
typename PredecessorMap, typename DistanceMap, typename WeightMap>
void
eager_dijkstra_shortest_paths
(const DistributedGraph& g,
typename graph_traits<DistributedGraph>::vertex_descriptor s,
PredecessorMap predecessor, DistanceMap distance,
typename property_traits<DistanceMap>::value_type lookahead,
WeightMap weight);
template<typename DistributedGraph, typename DijkstraVisitor,
typename PredecessorMap, typename DistanceMap>
void
eager_dijkstra_shortest_paths
(const DistributedGraph& g,
typename graph_traits<DistributedGraph>::vertex_descriptor s,
PredecessorMap predecessor, DistanceMap distance,
typename property_traits<DistanceMap>::value_type lookahead);
}
In each superstep, parallel Dijkstra's algorithm typically only processes nodes whose distances equivalent to the global minimum distance, because these distances are guaranteed to be correct. This variation on the algorithm allows the algorithm to process all vertices whose distances are within some constant value of the minimum distance. The value is called the "lookahead" value and is provided by the user as the fifth parameter to the function. Small values of the lookahead parameter will likely result in limited parallelization opportunities, whereas large values will expose more parallelism but may introduce (non-infinite) looping and result in extra work. The optimal value for the lookahead parameter depends on the input graph; see [CMMS98b] and [MS98].
This algorithm will be used by dijkstra_shortest_paths() when it is provided with a lookahead value.
<boost/graph/distributed/eager_dijkstra_shortest_paths.hpp>
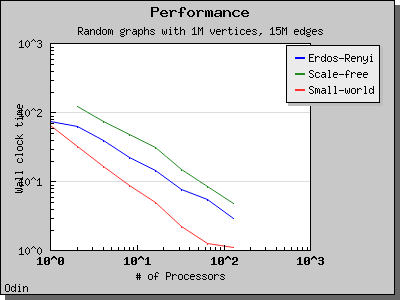
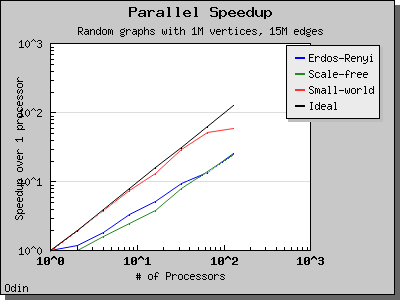
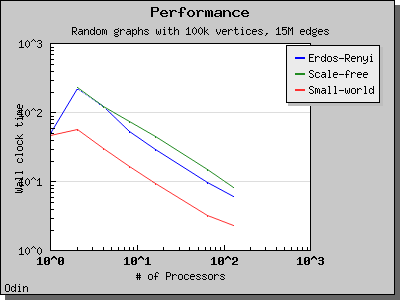
This algorithm performs O(V log V) work in d + 1 BSP supersteps, where d is at most O(V) but may be smaller depending on the lookahead value. the algorithm may perform more work when a large lookahead is provided, because vertices will be reprocessed.
The performance of the eager Dijkstra's algorithm varies greatly depending on the lookahead value. The following charts illustrate the performance of the Parallel BGL on graphs with edge weights uniformly selected from the range [0, 1) and a constant lookahead of 0.1.
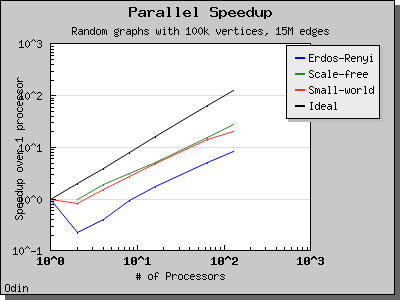
namespace boost { namespace graph { namespace distributed {
template <typename Graph, typename PredecessorMap,
typename DistanceMap, typename WeightMap>
void delta_stepping_shortest_paths
(const Graph& g,
typename graph_traits<Graph>::vertex_descriptor s,
PredecessorMap predecessor, DistanceMap distance, WeightMap weight,
typename property_traits<WeightMap>::value_type delta)
template <typename Graph, typename PredecessorMap,
typename DistanceMap, typename WeightMap>
void delta_stepping_shortest_paths
(const Graph& g,
typename graph_traits<Graph>::vertex_descriptor s,
PredecessorMap predecessor, DistanceMap distance, WeightMap weight)
}
} } }
The delta-stepping algorithm [MS98] is another variant of the parallel Dijkstra algorithm. Like the eager Dijkstra algorithm, it employs a lookahead (delta) value that allows processors to process vertices before we are guaranteed to find their minimum distances, permitting more parallelism than a conservative strategy. Delta-stepping also introduces a multi-level bucket data structure that provides more relaxed ordering constraints than the priority queues employed by the other Dijkstra variants, reducing the complexity of insertions, relaxations, and removals from the central data structure. The delta-stepping algorithm is the best-performing of the Dijkstra variants.
The lookahead value delta determines how large each of the "buckets" within the delta-stepping queue will be, where the ith bucket contains edges within tentative distances between delta``*i and ``delta``*(i+1). ``delta must be a positive value. When omitted, delta will be set to the maximum edge weight divided by the maximum degree.
<boost/graph/distributed/delta_stepping_shortest_paths.hpp>
See the separate Dijkstra example.
| [CMMS98a] | Andreas Crauser, Kurt Mehlhorn, Ulrich Meyer, and Peter Sanders. A Parallelization of Dijkstra's Shortest Path Algorithm. In Mathematical Foundations of Computer Science (MFCS), volume 1450 of Lecture Notes in Computer Science, pages 722--731, 1998. Springer. |
| [CMMS98b] | Andreas Crauser, Kurt Mehlhorn, Ulrich Meyer, and Peter Sanders. Parallelizing Dijkstra's shortest path algorithm. Technical report, MPI-Informatik, 1998. |
| [MS98] | (1, 2) Ulrich Meyer and Peter Sanders. Delta-stepping: A parallel shortest path algorithm. In 6th ESA, LNCS. Springer, 1998. |
Copyright (C) 2004, 2005, 2006, 2007, 2008 The Trustees of Indiana University.
Authors: Douglas Gregor and Andrew Lumsdaine