 Boost
C++ Libraries
Boost
C++ Libraries
...one of the most highly
regarded and expertly designed C++ library projects in the
world.
— Herb Sutter and Andrei
Alexandrescu, C++
Coding Standards
 Boost
C++ Libraries
Boost
C++ Libraries
...one of the most highly
regarded and expertly designed C++ library projects in the
world.
— Herb Sutter and Andrei
Alexandrescu, C++
Coding Standards
 Connected Components
Connected Components
namespace graph {
// Default constructed ParentMap
template<typename Graph, typename ComponentMap, typename ParentMap>
typename property_traits<ComponentMap>::value_type
connected_components( const Graph& g, ComponentMap c);
// User supplied ParentMap
template<typename Graph, typename ComponentMap, typename ParentMap>
typename property_traits<ComponentMap>::value_type
connected_components( const Graph& g, ComponentMap c, ParentMap p);
}
The connected_components() function computes the connected components of an undirected graph. The distributed connected components algorithm uses the sequential version of the connected components algorithm to compute the connected components of the local subgraph, then executes the parallel phase of the algorithm. The parallel portion of the connected components algorithm is loosely based on the work of Goddard, Kumar, and Prins. The interface is a superset of the interface to the BGL sequential connected components algorithm.
Prior to executing the sequential phase of the algorithm, each process identifies the roots of its local components. An adjacency list of all vertices adjacent to members of the component is then constructed at the root vertex of each component.
The parallel phase of the distributed connected components algorithm consists of a series of supersteps. In each superstep, each root attempts to hook to a member of it's adjacency list by assigning it's parent pointer to that vertex. Hooking is restricted to vertices which are logically less than the current vertex to prevent looping. Vertices which hook successfully are removed from the list of roots and placed on another list of completed vertices. All completed vertices now execute a pointer jumping step until every completed vertex has as its parent the root of a component. This pointer jumping step may be further optimized by the addition of Cycle Reduction (CR) rules developed by Johnson and Metaxas, however current performance evaluations indicate that this would have a negligible impact on the overall performance of the algorithm. These CR rules reduce the number of pointer jumping steps from O(n) to O(log n). Following this pointer jumping step, roots which have hooked in this phase transmit their adjacency list to their new parent. The remaining roots receive these edges and execute a pruning step on their adjacency lists to remove vertices that are now members of their component. The parallel phase of the algorithm is complete when no root successfully hooks. Once the parallel phase is complete a final pointer jumping step is performed on all vertices to assign the parent pointers of the leaves of the initial local subgraph components to their final parent which has now been determined.
The single largest performance bottleneck in the distributed connected components algorithm is the effect of poor vertex distribution on the algorithm. For sparse graphs with a single large component, many roots may hook to the same component, resulting in severe load imbalance at the process owning this component. Several methods of modifying the hooking strategy to avoid this behavior have been implemented but none has been successful as of yet.
Contents
<boost/graph/connected_components.hpp>
The local phase of the algorithm is O(V + E). The parallel phase of the algorithm requires at most O(d) supersteps where d is the number of initial roots. d is at most O(V) but becomes significantly smaller as E increases. The pointer jumping phase within each superstep requires at most O(c) steps on each of the completed roots where c is the length of the longest cycle. Application of CR rules can reduce this to O(log c).
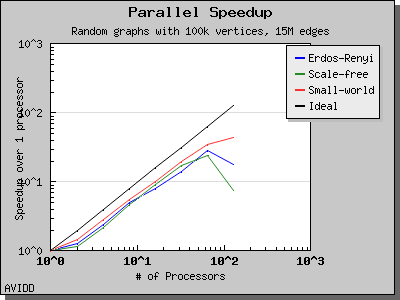
The following charts illustrate the performance of the Parallel BGL connected components algorithm. It performs well on very sparse and very dense graphs. However, for cases where the graph has a medium density with a giant connected component, the algorithm will perform poorly. This is a known problem with the algorithm and as far as we know all implemented algorithms have this degenerate behavior.
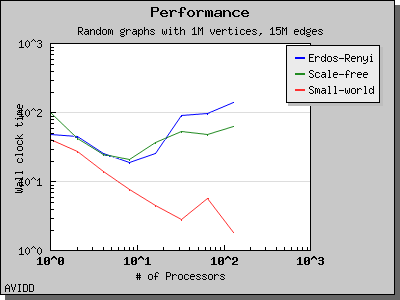
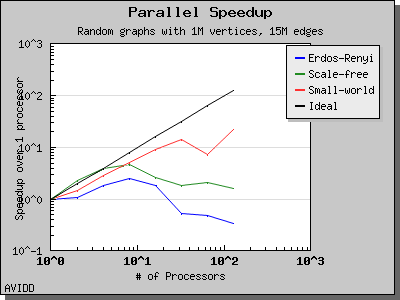
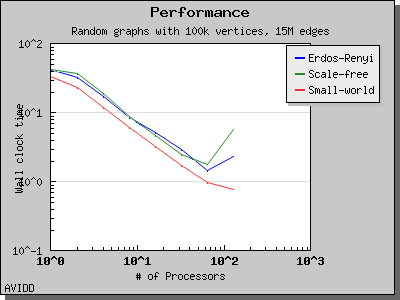
Copyright (C) 2004 The Trustees of Indiana University.
Authors: Nick Edmonds, Douglas Gregor, and Andrew Lumsdaine