 Boost
C++ Libraries
Boost
C++ Libraries
...one of the most highly
regarded and expertly designed C++ library projects in the
world.
— Herb Sutter and Andrei
Alexandrescu, C++
Coding Standards
 Boost
C++ Libraries
Boost
C++ Libraries
...one of the most highly
regarded and expertly designed C++ library projects in the
world.
— Herb Sutter and Andrei
Alexandrescu, C++
Coding Standards
 Minimum Spanning Tree
Minimum Spanning TreeThe Parallel BGL contains four minimum spanning tree (MST) algorithms [DG98] for use on undirected, weighted, distributed graphs. The graphs need not be connected: each algorithm will compute a minimum spanning forest (MSF) when provided with a disconnected graph.
The interface to each of the four algorithms is similar to the implementation of 'Kruskal's algorithm'_ in the sequential BGL. Each accepts, at a minimum, a graph, a weight map, and an output iterator. The edges of the MST (or MSF) will be output via the output iterator on process 0: other processes may receive edges on their output iterators, but the set may not be complete, depending on the algorithm. The algorithm parameters are documented together, because they do not vary greatly. See the section Selecting an MST algorithm for advice on algorithm selection.
The graph itself must model the Vertex List Graph concept and the Distributed Edge List Graph concept. Since the most common distributed graph structure, the distributed adjacency list, only models the Distributed Vertex List Graph concept, it may only be used with these algorithms when wrapped in a suitable adaptor, such as the vertex_list_adaptor.
Contents
<boost/graph/distributed/dehne_gotz_min_spanning_tree.hpp>
A mapping from vertex descriptors to indices in the range [0, num_vertices(g)). This must be a Readable Property Map whose key type is a vertex descriptor and whose value type is an integral type, typically the vertices_size_type of the graph.
Default: get(vertex_index, g)
Stores the rank of each vertex, which is used for maintaining union-find data structures. This must be a Read/Write Property Map whose key type is a vertex descriptor and whose value type is an integral type.
Default: An iterator_property_map built from an STL vector of the vertices_size_type of the graph and the vertex index map.
Stores the parent (representative) of each vertex, which is used for maintaining union-find data structures. This must be a Read/Write Property Map whose key type is a vertex descriptor and whose value type is also a vertex descriptor.
Default: An iterator_property_map built from an STL vector of the vertex_descriptor of the graph and the vertex index map.
Stores the supervertex index of each vertex, which is used for maintaining the supervertex list data structures. This must be a Read/Write Property Map whose key type is a vertex descriptor and whose value type is an integral type.
Default: An iterator_property_map built from an STL vector of the vertices_size_type of the graph and the vertex index map.
namespace graph {
template<typename Graph, typename WeightMap, typename OutputIterator,
typename VertexIndexMap, typename RankMap, typename ParentMap,
typename SupervertexMap>
OutputIterator
dense_boruvka_minimum_spanning_tree(const Graph& g, WeightMap weight_map,
OutputIterator out,
VertexIndexMap index,
RankMap rank_map, ParentMap parent_map,
SupervertexMap supervertex_map);
template<typename Graph, typename WeightMap, typename OutputIterator,
typename VertexIndex>
OutputIterator
dense_boruvka_minimum_spanning_tree(const Graph& g, WeightMap weight_map,
OutputIterator out, VertexIndex index);
template<typename Graph, typename WeightMap, typename OutputIterator>
OutputIterator
dense_boruvka_minimum_spanning_tree(const Graph& g, WeightMap weight_map,
OutputIterator out);
}
The dense Boruvka distributed minimum spanning tree algorithm is a direct parallelization of the sequential MST algorithm by Boruvka. The algorithm first creates a supervertex out of each vertex. Then, in each iteration, it finds the smallest-weight edge incident to each vertex, collapses supervertices along these edges, and removals all self loops. The only difference between the sequential and parallel algorithms is that the parallel algorithm performs an all-reduce operation so that all processes have the global minimum set of edges.
Unlike the other three algorithms, this algorithm emits the complete list of edges in the minimum spanning forest via the output iterator on all processes. It may therefore be more useful than the others when parallelizing sequential BGL programs.
The distributed algorithm requires O(log n) BSP supersteps, each of which requires O(m/p + n) time and O(n) communication per process.
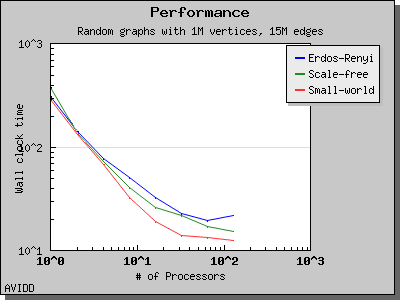
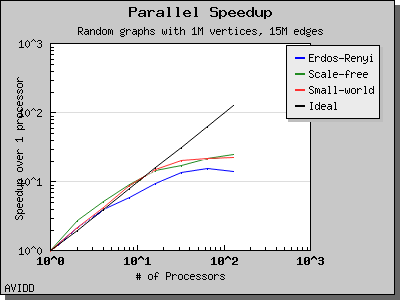
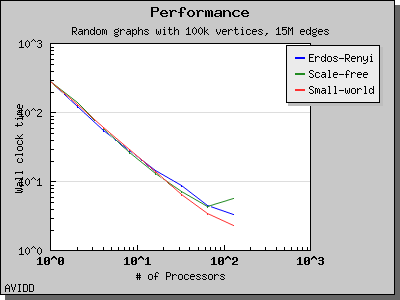
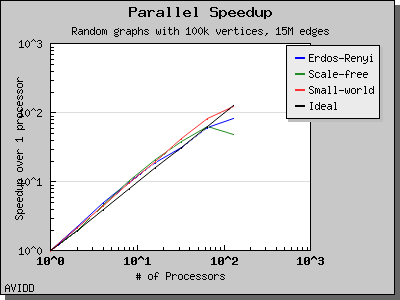
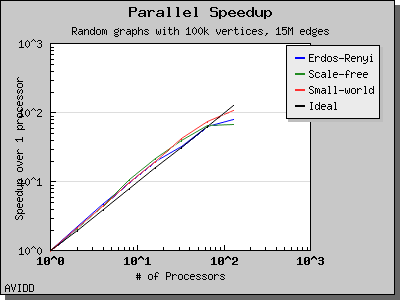
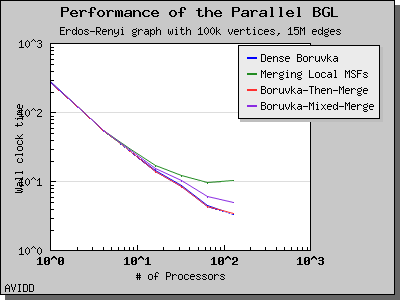
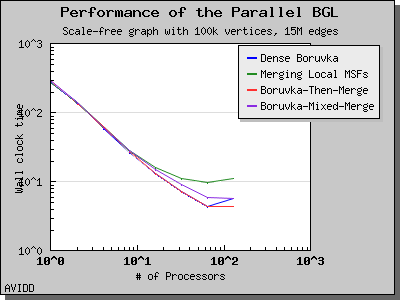
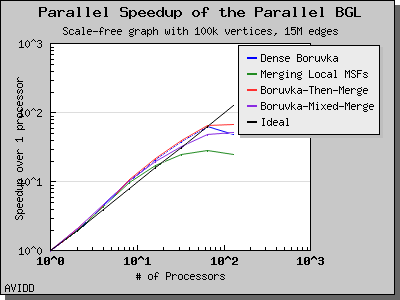
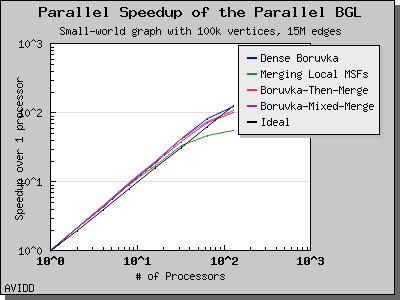
The following charts illustrate the performance of this algorithm on various random graphs. We see that the algorithm scales well up to 64 or 128 processors, depending on the type of graph, for dense graphs. However, for sparse graphs performance tapers off as the number of processors surpases m/n, i.e., the average degree (which is 30 for this graph). This behavior is expected from the algorithm.
namespace graph {
template<typename Graph, typename WeightMap, typename OutputIterator,
typename VertexIndexMap>
OutputIterator
merge_local_minimum_spanning_trees(const Graph& g, WeightMap weight,
OutputIterator out,
VertexIndexMap index);
template<typename Graph, typename WeightMap, typename OutputIterator>
inline OutputIterator
merge_local_minimum_spanning_trees(const Graph& g, WeightMap weight,
OutputIterator out);
}
The merging local MSTs algorithm operates by computing minimum spanning forests from the edges stored on each process. Then the processes merge their edge lists along a tree. The child nodes cease participating in the computation, but the parent nodes recompute MSFs from the newly acquired edges. In the final round, the root of the tree computes the global MSFs, having received candidate edges from every other process via the tree.
This algorithm requires O(log_D p) BSP supersteps (where D is the number of children in the tree, and is currently fixed at 3). Each superstep requires O((m/p) log (m/p) + n) time and O(m/p) communication per process.
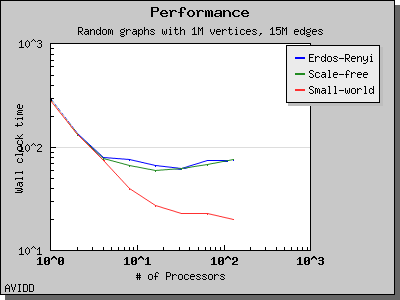
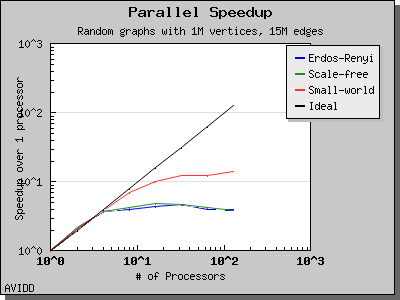
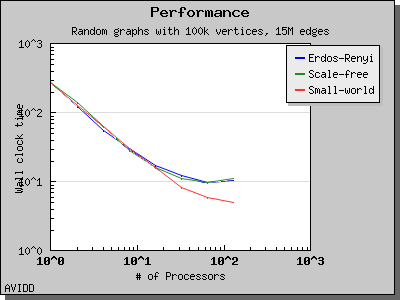
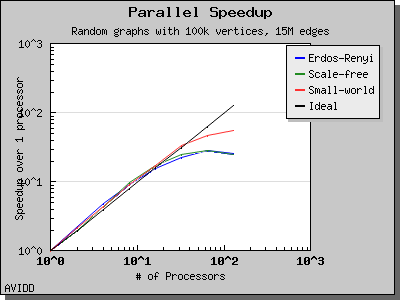
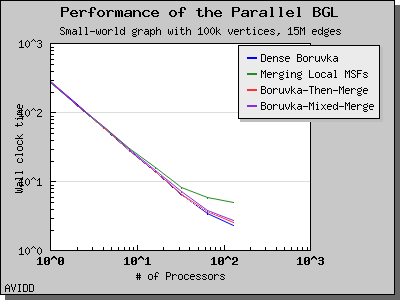
The following charts illustrate the performance of this algorithm on various random graphs. The algorithm only scales well for very dense graphs, where most of the work is performed in the initial stage and there is very little work in the later stages.
namespace graph {
template<typename Graph, typename WeightMap, typename OutputIterator,
typename VertexIndexMap, typename RankMap, typename ParentMap,
typename SupervertexMap>
OutputIterator
boruvka_then_merge(const Graph& g, WeightMap weight, OutputIterator out,
VertexIndexMap index, RankMap rank_map,
ParentMap parent_map, SupervertexMap
supervertex_map);
template<typename Graph, typename WeightMap, typename OutputIterator,
typename VertexIndexMap>
inline OutputIterator
boruvka_then_merge(const Graph& g, WeightMap weight, OutputIterator out,
VertexIndexMap index);
template<typename Graph, typename WeightMap, typename OutputIterator>
inline OutputIterator
boruvka_then_merge(const Graph& g, WeightMap weight, OutputIterator out);
}
This algorithm applies both Boruvka steps and local MSF merging steps together to achieve better asymptotic performance than either algorithm alone. It first executes Boruvka steps until only n/(log_d p)^2 supervertices remain, then completes the MSF computation by performing local MSF merging on the remaining edges and supervertices.
This algorithm requires log_D p + log log_D p BSP supersteps. The time required by each superstep depends on the type of superstep being performed; see the distributed Boruvka or merging local MSFS algorithms for details.
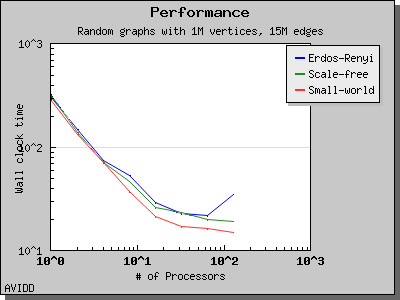
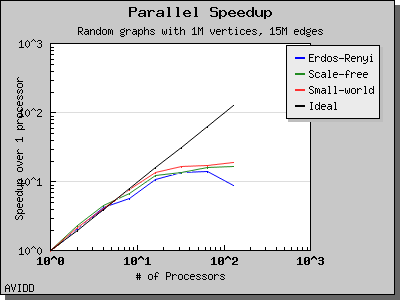
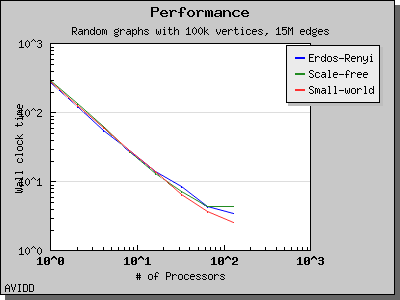
The following charts illustrate the performance of this algorithm on various random graphs. We see that the algorithm scales well up to 64 or 128 processors, depending on the type of graph, for dense graphs. However, for sparse graphs performance tapers off as the number of processors surpases m/n, i.e., the average degree (which is 30 for this graph). This behavior is expected from the algorithm.
namespace {
template<typename Graph, typename WeightMap, typename OutputIterator,
typename VertexIndexMap, typename RankMap, typename ParentMap,
typename SupervertexMap>
OutputIterator
boruvka_mixed_merge(const Graph& g, WeightMap weight, OutputIterator out,
VertexIndexMap index, RankMap rank_map,
ParentMap parent_map, SupervertexMap
supervertex_map);
template<typename Graph, typename WeightMap, typename OutputIterator,
typename VertexIndexMap>
inline OutputIterator
boruvka_mixed_merge(const Graph& g, WeightMap weight, OutputIterator out,
VertexIndexMap index);
template<typename Graph, typename WeightMap, typename OutputIterator>
inline OutputIterator
boruvka_mixed_merge(const Graph& g, WeightMap weight, OutputIterator out);
}
This algorithm applies both Boruvka steps and local MSF merging steps together to achieve better asymptotic performance than either method alone. In each iteration, the algorithm first performs a Boruvka step and then merges the local MSFs computed based on the supervertex graph.
This algorithm requires log_D p BSP supersteps. The time required by each superstep depends on the type of superstep being performed; see the distributed Boruvka or merging local MSFS algorithms for details. However, the algorithm is communication-optional (requiring O(n) communication overall) when the graph is sufficiently dense, i.e., m/n >= p.
The following charts illustrate the performance of this algorithm on various random graphs. We see that the algorithm scales well up to 64 or 128 processors, depending on the type of graph, for dense graphs. However, for sparse graphs performance tapers off as the number of processors surpases m/n, i.e., the average degree (which is 30 for this graph). This behavior is expected from the algorithm.
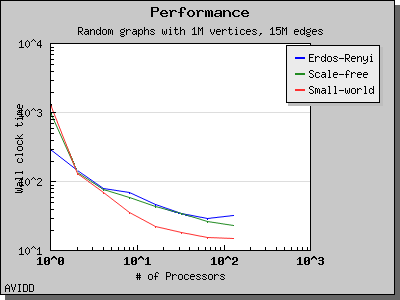
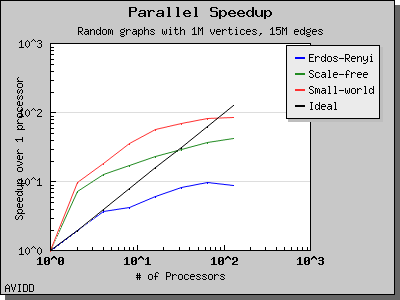
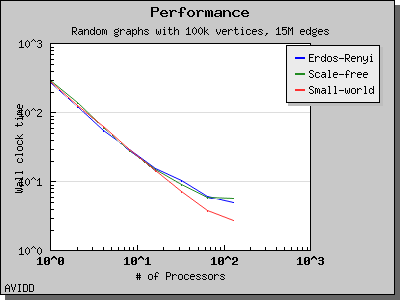
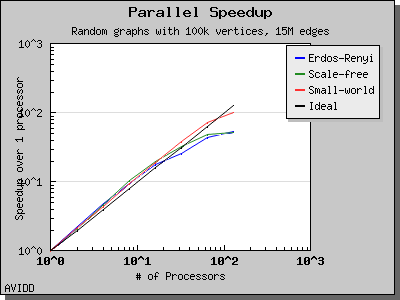
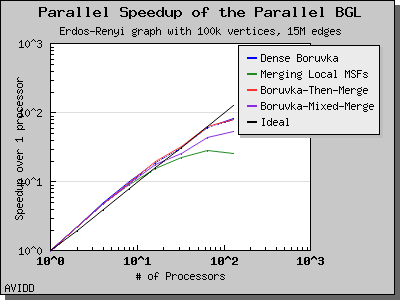
Dehne and Gotz reported [DG98] mixed results when evaluating these four algorithms. No particular algorithm was clearly better than the others in all cases. However, the asymptotically best algorithm (boruvka_mixed_merge) seemed to perform more poorly in their tests than the other merging-based algorithms. The following performance charts illustrate the performance of these four minimum spanning tree implementations.
Overall, dense_boruvka_minimum_spanning_tree gives the most consistent performance and scalability for the graphs we tested. Additionally, it may be more suitable for sequential programs that are being parallelized, because it emits complete MSF edge lists via the output iterators in every process.
Copyright (C) 2004 The Trustees of Indiana University.
Authors: Douglas Gregor and Andrew Lumsdaine
| [DG98] | (1, 2) Frank Dehne and Silvia Gotz. Practical Parallel Algorithms for Minimum Spanning Trees. In Symposium on Reliable Distributed Systems, pages 366--371, 1998. |