 Boost
C++ Libraries
Boost
C++ Libraries
...one of the most highly
regarded and expertly designed C++ library projects in the
world.
— Herb Sutter and Andrei
Alexandrescu, C++
Coding Standards
 Boost
C++ Libraries
Boost
C++ Libraries
...one of the most highly
regarded and expertly designed C++ library projects in the
world.
— Herb Sutter and Andrei
Alexandrescu, C++
Coding Standards
#include <boost/math/distributions/rayleigh.hpp>
namespace boost{ namespace math{ template <class RealType = double, class Policy = policies::policy<> > class rayleigh_distribution; typedef rayleigh_distribution<> rayleigh; template <class RealType, class Policy> class rayleigh_distribution { public: typedef RealType value_type; typedef Policy policy_type; // Construct: rayleigh_distribution(RealType sigma = 1) // Accessors: RealType sigma()const; }; }} // namespaces
The Rayleigh distribution is a continuous distribution with the probability density function:
f(x; sigma) = x * exp(-x2/2 σ2) / σ2
For sigma parameter σ > 0, and x > 0.
The Rayleigh distribution is often used where two orthogonal components have an absolute value, for example, wind velocity and direction may be combined to yield a wind speed, or real and imaginary components may have absolute values that are Rayleigh distributed.
The following graph illustrates how the Probability density Function(pdf) varies with the shape parameter σ:
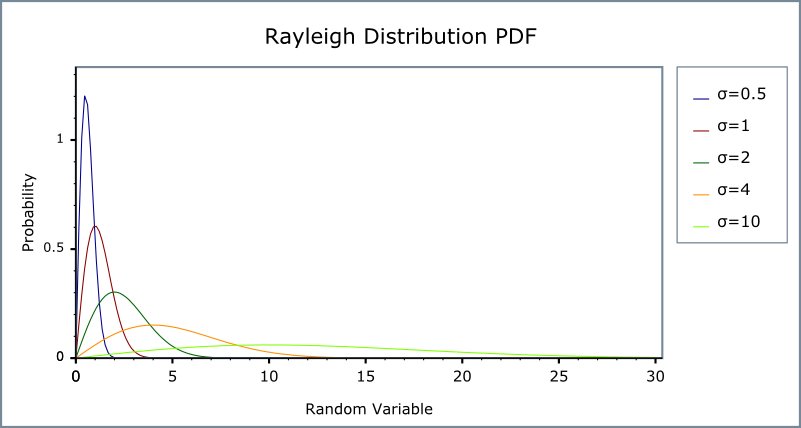
and the Cumulative Distribution Function (cdf)

The absolute value of two independent normal distributions X and Y, √ (X2 + Y2) is a Rayleigh distribution.
The Chi, Rice and Weibull distributions are generalizations of the Rayleigh distribution.
rayleigh_distribution(RealType sigma = 1);
Constructs a Rayleigh distribution with σ sigma.
Requires that the σ parameter is greater than zero, otherwise calls domain_error.
RealType sigma()const;
Returns the sigma parameter of this distribution.
All the usual non-member accessor functions that are generic to all distributions are supported: Cumulative Distribution Function, Probability Density Function, Quantile, Hazard Function, Cumulative Hazard Function, mean, median, mode, variance, standard deviation, skewness, kurtosis, kurtosis_excess, range and support.
The domain of the random variable is [0, max_value].
The Rayleigh distribution is implemented in terms of the standard library
sqrt and exp and as such should have very low
error rates. Some constants such as skewness and kurtosis were calculated
using NTL RR type with 150-bit accuracy, about 50 decimal digits.
In the following table σ is the sigma parameter of the distribution, x is the random variate, p is the probability and q = 1-p.
|
Function |
Implementation Notes |
|---|---|
|
|
Using the relation: pdf = x * exp(-x2)/2 σ2 |
|
cdf |
Using the relation: p = 1 - exp(-x2/2) σ2 = -expm1(-x2/2) σ2 |
|
cdf complement |
Using the relation: q = exp(-x2/ 2) * σ2 |
|
quantile |
Using the relation: x = sqrt(-2 * σ 2) * log(1 - p)) = sqrt(-2 * σ 2) * log1p(-p)) |
|
quantile from the complement |
Using the relation: x = sqrt(-2 * σ 2) * log(q)) |
|
mean |
σ * sqrt(π/2) |
|
variance |
σ2 * (4 - π/2) |
|
mode |
σ |
|
skewness |
Constant from Weisstein, Eric W. "Weibull Distribution." From MathWorld--A Wolfram Web Resource. |
|
kurtosis |
Constant from Weisstein, Eric W. "Weibull Distribution." From MathWorld--A Wolfram Web Resource. |
|
kurtosis excess |
Constant from Weisstein, Eric W. "Weibull Distribution." From MathWorld--A Wolfram Web Resource. |