 Boost
C++ Libraries
Boost
C++ Libraries
...one of the most highly
regarded and expertly designed C++ library projects in the
world.
— Herb Sutter and Andrei
Alexandrescu, C++
Coding Standards
 Boost
C++ Libraries
Boost
C++ Libraries
...one of the most highly
regarded and expertly designed C++ library projects in the
world.
— Herb Sutter and Andrei
Alexandrescu, C++
Coding Standards
#include <boost/math/special_functions/airy.hpp>
namespace boost { namespace math { template <class T> calculated-result-type airy_bi(T x); template <class T, class Policy> calculated-result-type airy_bi(T x, const Policy&); }} // namespaces
The function airy_bi calculates the Airy function Bi which is the second solution to the differential equation:
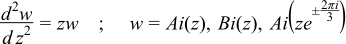
The final Policy argument is optional and can be used to control the behaviour of the function: how it handles errors, what level of precision to use etc. Refer to the policy documentation for more details.
The following graph illustrates how this function changes as x changes: for negative x the function is cyclic, while for positive x the value tends to infinity:

This function is implemented entirely in terms of the Bessel functions cyl_bessel_i and cyl_bessel_j - refer to those functions for detailed accuracy information.
In general though, the relative error is low (less than 100 ε) for x > 0 while only the absolute error is low for x < 0.
Since this function is implemented in terms of other special functions, there are only a few basic sanity checks, using test values from functions.wolfram.com.
This function is implemented in terms of the Bessel functions using the relations:
