 Boost
C++ Libraries
Boost
C++ Libraries
...one of the most highly
regarded and expertly designed C++ library projects in the
world.
— Herb Sutter and Andrei
Alexandrescu, C++
Coding Standards
 Boost
C++ Libraries
Boost
C++ Libraries
...one of the most highly
regarded and expertly designed C++ library projects in the
world.
— Herb Sutter and Andrei
Alexandrescu, C++
Coding Standards
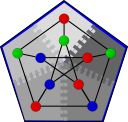 Boman et al graph coloring
Boman et al graph coloring
namespace graph {
template<typename DistributedGraph, typename ColorMap>
typename property_traits<ColorMap>::value_type
boman_et_al_graph_coloring
(const DistributedGraph& g,
ColorMap color,
typename graph_traits<DistributedGraph>::vertices_size_type s = 100);
template<typename DistributedGraph, typename ColorMap, typename ChooseColor>
typename property_traits<ColorMap>::value_type
boman_et_al_graph_coloring
(const DistributedGraph& g,
ColorMap color,
typename graph_traits<DistributedGraph>::vertices_size_type s,
ChooseColor choose_color);
template<typename DistributedGraph, typename ColorMap, typename ChooseColor,
typename VertexOrdering>
typename property_traits<ColorMap>::value_type
boman_et_al_graph_coloring
(const DistributedGraph& g, ColorMap color,
typename graph_traits<DistributedGraph>::vertices_size_type s,
ChooseColor choose_color, VertexOrdering ordering);
template<typename DistributedGraph, typename ColorMap, typename ChooseColor,
typename VertexOrdering, typename VertexIndexMap>
typename property_traits<ColorMap>::value_type
boman_et_al_graph_coloring
(const DistributedGraph& g,
ColorMap color,
typename graph_traits<DistributedGraph>::vertices_size_type s,
ChooseColor choose_color,
VertexOrdering ordering, VertexIndexMap vertex_index);
}
The boman_et_al_graph_coloring function colors the vertices of an undirected, distributed graph such that no two adjacent vertices have the same color. All of the vertices of a given color form an independent set in the graph. Graph coloring has been used to solve various problems, including register allocation in compilers, optimization problems, and scheduling problems.
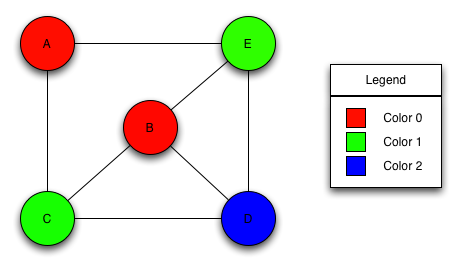
The problem of coloring a graph with the fewest possible number of colors is NP-complete, so many algorithms (including the one implemented here) are heuristic algorithms that try to minimize the number of colors but are not guaranteed to provide an optimal solution. This algorithm [BBC05] is similar to the sequential_vertex_coloring algorithm, that iterates through the vertices once and selects the lowest-numbered color that the current vertex can have. The coloring and the number of colors is therefore related to the ordering of the vertices in the sequential case.
The distributed boman_et_al_graph_coloring algorithm will produce different colorings depending on the ordering and distribution of the vertices and the number of parallel processes cooperating to perform the coloring.
The algorithm returns the number of colors num_colors used to color the graph.
Contents
<boost/graph/distributed/boman_et_al_graph_coloring.hpp>
The number of vertices to color within each superstep. After s vertices have been colored, the colors of boundary vertices will be sent to their out-of-process neighbors. Smaller values communicate more often but may reduce the risk of conflicts, whereas larger values do more work in between communication steps but may create many conflicts.
Default: 100
A function object that chooses the color for a vertex given the colors of its neighbors. The function object will be passed a vector of values (marked) and a marked_true value, and should return a color value such that color >= marked.size() or marked[color] != marked_true.
Default: boost::graph::distributed::first_fit_color<color_type>(), where color_type is the value type of the ColorMap property map.
A binary predicate function object that provides total ordering on the vertices in the graph. Whenever a conflict arises, only one of the processes involved will recolor the vertex in the next round, and this ordering determines which vertex should be considered conflicting (its owning process will then handle the conflict). Ideally, this predicate should order vertices so that conflicting vertices will be spread uniformly across processes. However, this predicate must resolve the same way on both processors.
Default: unspecified
A mapping from vertex descriptors to indices in the range [0, num_vertices(g)). This must be a Readable Property Map whose key type is a vertex descriptor and whose value type is an integral type, typically the vertices_size_type of the graph.
Default: get(vertex_index, g)
The complexity of this algorithm is hard to characterize, because it depends greatly on the number of conflicts that occur during the algorithm. A conflict occurs when a boundary vertex (i.e., a vertex that is adjacent to a vertex stored on a different processor) is given the same color is a boundary vertex adjacency to it (but on another processor). Conflicting vertices must be assigned new colors, requiring additional work and communication. The work involved in reassigning a color for a conflicting vertex is O(d), where d is the degree of the vertex and O(1) messages of O(1) size are needed to resolve the conflict. Note that the number of conflicts grows with (1) the number of processes and (2) the number of inter-process edges.
The performance of this implementation of Bomen et al's graph coloring algorithm is illustrated by the following charts. Scaling and performance is reasonable for all of the graphs we have tried.
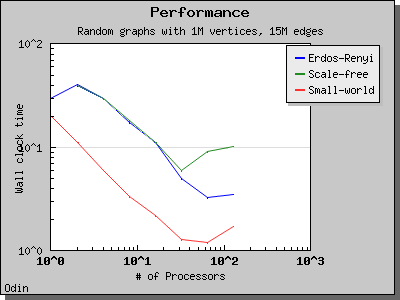
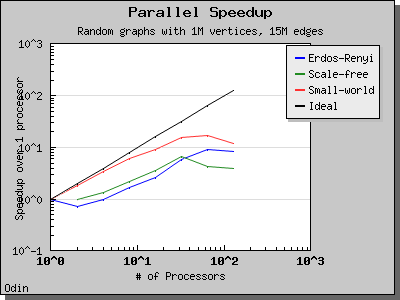
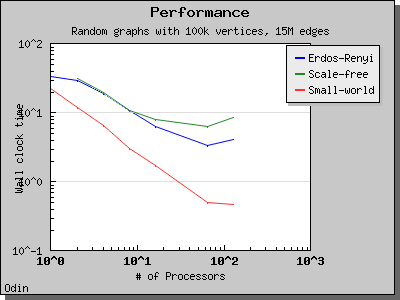
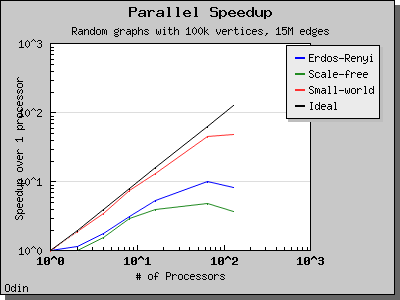
Copyright (C) 2005 The Trustees of Indiana University.
Authors: Douglas Gregor and Andrew Lumsdaine
| [BBC05] | Erik G. Boman, Doruk Bozdag, Umit Catalyurek, Assefaw H. Gebremedhin, and Fredrik Manne. A Scalable Parallel Graph Coloring Algorithm for Distributed Memory Computers. [preprint] |