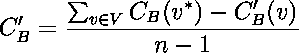Boost Graph Library: Brandes' Betweenness Centrality
brandes_betweenness_centrality
// named parameter versions
template<typename Graph, typename Param, typename Tag, typename Rest>
void
brandes_betweenness_centrality(const Graph& g,
const bgl_named_params<Param,Tag,Rest>& params);
template<typename Graph, typename CentralityMap>
void
brandes_betweenness_centrality(const Graph& g, CentralityMap centrality_map);
template<typename Graph, typename CentralityMap, typename EdgeCentralityMap>
void
brandes_betweenness_centrality(const Graph& g, CentralityMap centrality_map,
EdgeCentralityMap edge_centrality);
// non-named parameter versions
template<typename Graph, typename CentralityMap, typename EdgeCentralityMap,
typename IncomingMap, typename DistanceMap, typename DependencyMap,
typename PathCountMap, typename VertexIndexMap>
void
brandes_betweenness_centrality(const Graph& g, CentralityMap centrality_map,
EdgeCentralityMap edge_centrality,
IncomingMap incoming,
DistanceMap distance, DependencyMap dependency,
PathCountMap path_count,
VertexIndexMap vertex_index);
template<typename Graph, typename CentralityMap, typename EdgeCentralityMap,
typename IncomingMap, typename DistanceMap, typename DependencyMap,
typename PathCountMap, typename VertexIndexMap, typename WeightMap>
void
brandes_betweenness_centrality(const Graph& g, CentralityMap centrality_map,
EdgeCentralityMap edge_centrality,
IncomingMap incoming,
DistanceMap distance, DependencyMap dependency,
PathCountMap path_count,
VertexIndexMap vertex_index,
WeightMap weight_map);
// helper functions
template<typename Graph, typename CentralityMap>
void
relative_betweenness_centrality(const Graph& g, CentralityMap centrality_map);
template<typename Graph, typename CentralityMap>
typename property_traits<CentralityMap>::value_type
central_point_dominance(const Graph& g, CentralityMap centrality_map);
This algorithm [54]
computes the betweenness centrality [55,56] of each vertex or each
edge in the graph. The betweenness centrality of a vertex v
is defined by
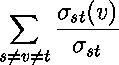 ,
,
where 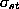 is the number of shortest paths from
vertex s to vertex t and
is the number of shortest paths from
vertex s to vertex t and 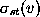 is the number of shortest paths from vertex s to vertex
t that pass through vertex v.
is the number of shortest paths from vertex s to vertex
t that pass through vertex v.
The edge betweenness centrality indicates for each edge the
betweenness centrality that was contributed to the target(s) of the
edge (plural for undirected graphs). Similar to (vertex) betweenness
centrality, edge betweenness centrality can be used to determine the
edges through which most shortest paths must pass. A single invocation
of this algorithm can compute either the vertex or edge centrality (or
both).
This algorithm can operate either on weighted graphs (if a suitable
edge weight map is supplied) or unweighted graphs (if no edge weight
map is supplied). The result is the absolute betweenness centrality;
to convert to the relative betweenness centrality, which scales each
absolute centrality by 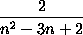 (where n is the number of vertices in the graph), use
relative_betweenness_centrality. Given the relative
betweenness centrality, one can compute the central point
dominance [55], which is a measure of the maximum "betweenness" of any
point in the graph: it will be 0 for complete graphs and
1 for "wheel" graphs (in which there is a central vertex that all
paths include; see Fig. 1). Let
(where n is the number of vertices in the graph), use
relative_betweenness_centrality. Given the relative
betweenness centrality, one can compute the central point
dominance [55], which is a measure of the maximum "betweenness" of any
point in the graph: it will be 0 for complete graphs and
1 for "wheel" graphs (in which there is a central vertex that all
paths include; see Fig. 1). Let 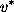 be the vertex with the largest relative betweenness centrality; then, the central point dominance is defined as:
be the vertex with the largest relative betweenness centrality; then, the central point dominance is defined as:
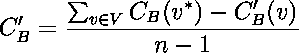
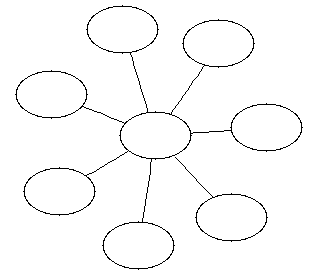
Fig. 1: A wheel graph, where every path travels through the central node.
The central point dominance of this graph is 1.
|
 |
Where Defined
boost/graph/betweenness_centrality.hpp
Parameters
IN:
const Graph& g
The graph object on which the algorithm will be applied. The type
Graph must be a model of Vertex List Graph and Incidence Graph. When an edge
centrality map is supplied, it must also model Edge List Graph.
UTIL:
IncomingMap incoming
This property map records the set of edges incoming to each vertex that comprise a shortest path from a particular source vertex through this vertex, and is used internally by the algorithm.The IncomingMap type must be a Lvalue Property
Map whose key type is the same as the vertex descriptor type of
the graph and whose value type is a Sequence (e.g., an
std::vector) containing edge descriptors.
Default:
iterator_property_map created from a
std::vector of std::vector<Edge>, where
Edge is the edge descriptor type of the graph.
UTIL:
DistanceMap distance_map
The shortest path weight from each source vertex s to each
vertex in the graph g is recorded in this property map, but
the result is only used internally. The type DistanceMap
must be a model of Read/Write
Property Map. The vertex descriptor type of the graph needs to
be usable as the key type of the distance map. The value type of the
distance map is the element type of a Monoid.
Default:
iterator_property_map created from a
std::vector of the WeightMap's value type (or the
vertices_size_type of the graph when no weight map exists)
of size num_vertices(g) and using the vertex_index for
the index map.
UTIL:
DependencyMap dependency
Property map used internally to accumulate partial betweenness
centrality results. The type DependencyMap must be a model
of Read/Write
Property Map. The vertex descriptor type of the graph needs to
be usable as the key type of the dependency map. The value type of
the dependency map must be compatible with the value type of the
centrality map.
Default:
iterator_property_map created from a
std::vector of the CentralityMap's value type of
size num_vertices(g) and using the vertex_index
for the index map.
UTIL:
PathCountMap path_count
Property map used internally to accumulate the number of paths that
pass through each particular vertex. The type PathCountMap
must be a model of Read/Write
Property Map. The vertex descriptor type of the graph needs to
be usable as the key type of the dependency map. The value type of
the dependency map must be an integral type large enough to store
the number of paths in the graph.
Default:
iterator_property_map created from a
std::vector of the degree_size_type of the graph of
size num_vertices(g) and using the vertex_index
for the index map.
Named parameters
OUT/UTIL:
CentralityMap centrality_map
This property map is used to accumulate the betweenness centrality
of each vertex, and is the primary output of the algorithm. The type
CentralityMap must be a model of Read/Write
Property Map, with the graph's vertex descriptor type as its key
type. The value type of this property map should be a floating-point
or rational type.
Default: a dummy_property_map, which requires no
work to compute and returns no answer.
OUT/UTIL:
EdgeCentralityMap edge_centrality
This property map is used to accumulate the betweenness centrality
of each edge, and is a secondary form of output for the
algorithm. The type EdgeCentralityMap must be a model of Read/Write
Property Map, with the graph's edge descriptor type as its key
type. The value type of this property map should be the same as the
value type of the CentralityMap property map.
Default: a dummy_property_map, which requires no
work to compute and returns no answer.
IN:
vertex_index_map(VertexIndexMap vertex_index)
This maps each vertex to an integer in the range [0,
num_vertices(g)). This is necessary for efficient updates of the
heap data structure when an edge is relaxed. The type
VertexIndexMap must be a model of
Readable Property Map. The value type of the map must be an
integer type. The vertex descriptor type of the graph needs to be
usable as the key type of the map.
Default: get(vertex_index, g)
IN:
weight_map(WeightMap w_map)
The weight or ``length'' of each edge in the graph. The weights
must all be non-negative, and the algorithm will throw a
negative_edge
exception is one of the edges is negative.
The type WeightMap must be a model of
Readable Property Map. The edge descriptor type of
the graph needs to be usable as the key type for the weight
map. The value type for this map must be
the same as the value type of the distance map.
Default: All edge weights are assumed to be equivalent.
Complexity
The time complexity is
O(VE) for unweighted graphs and
O(VE + V(V+E) log V) for weighted graphs. The space complexity
is
O(VE).
Last modified: Wed Aug 4 17:41:44 EST 2004
 Boost
C++ Libraries
Boost
C++ Libraries
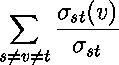 ,
,
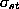 is the number of shortest paths from
vertex s to vertex t and
is the number of shortest paths from
vertex s to vertex t and 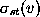 is the number of shortest paths from vertex s to vertex
t that pass through vertex v.
is the number of shortest paths from vertex s to vertex
t that pass through vertex v.
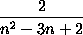 (where n is the number of vertices in the graph), use
relative_betweenness_centrality. Given the relative
betweenness centrality, one can compute the central point
dominance [
(where n is the number of vertices in the graph), use
relative_betweenness_centrality. Given the relative
betweenness centrality, one can compute the central point
dominance [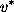 be the vertex with the largest relative betweenness centrality; then, the central point dominance is defined as:
be the vertex with the largest relative betweenness centrality; then, the central point dominance is defined as: