 Boost
C++ Libraries
Boost
C++ Libraries
...one of the most highly
regarded and expertly designed C++ library projects in the
world.
— Herb Sutter and Andrei
Alexandrescu, C++
Coding Standards
 Boost
C++ Libraries
Boost
C++ Libraries
...one of the most highly
regarded and expertly designed C++ library projects in the
world.
— Herb Sutter and Andrei
Alexandrescu, C++
Coding Standards
template <class T1, class T2> calculated-result-type cyl_bessel_j(T1 v, T2 x); template <class T1, class T2, class Policy> calculated-result-type cyl_bessel_j(T1 v, T2 x, const Policy&); template <class T1, class T2> calculated-result-type cyl_neumann(T1 v, T2 x); template <class T1, class T2, class Policy> calculated-result-type cyl_neumann(T1 v, T2 x, const Policy&);
The functions cyl_bessel_j and cyl_neumann return the result of the Bessel functions of the first and second kinds respectively:
cyl_bessel_j(v, x) = Jv(x)
cyl_neumann(v, x) = Yv(x) = Nv(x)
where:


The return type of these functions is computed using the result type calculation rules when T1 and T2 are different types. The functions are also optimised for the relatively common case that T1 is an integer.
The final Policy argument is optional and can be used to control the behaviour of the function: how it handles errors, what level of precision to use etc. Refer to the policy documentation for more details.
The functions return the result of domain_error
whenever the result is undefined or complex. For cyl_bessel_j
this occurs when x <
0 and v is not an integer, or when
x ==
0 and v
!= 0.
For cyl_neumann
this occurs when x <=
0.
The following graph illustrates the cyclic nature of Jv:

The following graph shows the behaviour of Yv: this is also cyclic for large x, but tends to -∞ for small x:

There are two sets of test values: spot values calculated using functions.wolfram.com, and a much larger set of tests computed using a simplified version of this implementation (with all the special case handling removed).
The following tables show how the accuracy of these functions varies on various platforms, along with comparisons to the GSL-1.9 and Cephes libraries. Note that the cyclic nature of these functions means that they have an infinite number of irrational roots: in general these functions have arbitrarily large relative errors when the arguments are sufficiently close to a root. Of course the absolute error in such cases is always small. Note that only results for the widest floating-point type on the system are given as narrower types have effectively zero error. All values are relative errors in units of epsilon.
Table 39. Errors Rates in cyl_bessel_j
|
Significand Size |
Platform and Compiler |
J0 and J1 |
Jv |
Jv (large values of x > 1000) |
|---|---|---|---|---|
|
53 |
Win32 / Visual C++ 8.0 |
Peak=2.5 Mean=1.1 GSL Peak=6.6 Cephes Peak=2.5 Mean=1.1 |
Peak=11 Mean=2.2 GSL Peak=11 Cephes Peak=17 Mean=2.5 |
Peak=413 Mean=110 GSL Peak=6x1011 Cephes Peak=2x105 |
|
64 |
Red Hat Linux IA64 / G++ 3.4 |
Peak=7 Mean=3 |
Peak=117 Mean=10 |
Peak=2x104 Mean=6x103 |
|
64 |
SUSE Linux AMD64 / G++ 4.1 |
Peak=7 Mean=3 |
Peak=400 Mean=40 |
Peak=2x104 Mean=1x104 |
|
113 |
HP-UX / HP aCC 6 |
Peak=14 Mean=6 |
Peak=29 Mean=3 |
Peak=2700 Mean=450 |
Table 40. Errors Rates in cyl_neumann
|
Significand Size |
Platform and Compiler |
J0 and J1 |
Jn (integer orders) |
Jv (fractional orders) |
|---|---|---|---|---|
|
53 |
Win32 / Visual C++ 8.0 |
Peak=330 Mean=54 GSL Peak=34 Mean=9 Cephes Peak=330 Mean=54 |
Peak=923 Mean=83 GSL Peak=500 Mean=54 Cephes Peak=923 Mean=83 |
Peak=561 Mean=36 GSL Peak=1.4x106 Mean=7x104 Cephes Peak=+INF |
|
64 |
Red Hat Linux IA64 / G++ 3.4 |
Peak=470 Mean=56 |
Peak=843 Mean=51 |
Peak=741 Mean=51 |
|
64 |
SUSE Linux AMD64 / G++ 4.1 |
Peak=1300 Mean=424 |
Peak=2x104 Mean=8x103 |
Peak=1x105 Mean=6x103 |
|
113 |
HP-UX / HP aCC 6 |
Peak=180 Mean=63 |
Peak=340 Mean=150 |
Peak=2x104 Mean=1200 |
Note that for large x these functions are largely
dependent on the accuracy of the std::sin
and std::cos functions.
Comparison to GSL and Cephes is interesting: both Cephes and this library optimise the integer order case - leading to identical results - simply using the general case is for the most part slightly more accurate though, as noted by the better accuracy of GSL in the integer argument cases. This implementation tends to perform much better when the arguments become large, Cephes in particular produces some remarkably inaccurate results with some of the test data (no significant figures correct), and even GSL performs badly with some inputs to Jv. Note that by way of double-checking these results, the worst performing Cephes and GSL cases were recomputed using functions.wolfram.com, and the result checked against our test data: no errors in the test data were found.
The implementation is mostly about filtering off various special cases:
When x is negative, then the order v must be an integer or the result is a domain error. If the order is an integer then the function is odd for odd orders and even for even orders, so we reflect to x > 0.
When the order v is negative then the reflection formulae can be used to move to v > 0:


Note that if the order is an integer, then these formulae reduce to:
J-n = (-1)nJn
Y-n = (-1)nYn
However, in general, a negative order implies that we will need to compute both J and Y.
When x is large compared to the order v then the asymptotic expansions for large x in M. Abramowitz and I.A. Stegun, Handbook of Mathematical Functions 9.2.19 are used (these were found to be more reliable than those in A&S 9.2.5).
When the order v is an integer the method first relates the result to J0, J1, Y0 and Y1 using either forwards or backwards recurrence (Miller's algorithm) depending upon which is stable. The values for J0, J1, Y0 and Y1 are calculated using the rational minimax approximations on root-bracketing intervals for small |x| and Hankel asymptotic expansion for large |x|. The coefficients are from:
W.J. Cody, ALGORITHM 715: SPECFUN - A Portable FORTRAN Package of Special Function Routines and Test Drivers, ACM Transactions on Mathematical Software, vol 19, 22 (1993).
and
J.F. Hart et al, Computer Approximations, John Wiley & Sons, New York, 1968.
These approximations are accurate to around 19 decimal digits: therefore these methods are not used when type T has more than 64 binary digits.
When x is smaller than machine epsilon then the following approximations for Y0(x), Y1(x), Y2(x) and Yn(x) can be used (see: http://functions.wolfram.com/03.03.06.0037.01, http://functions.wolfram.com/03.03.06.0038.01, http://functions.wolfram.com/03.03.06.0039.01 and http://functions.wolfram.com/03.03.06.0040.01):




When x is small compared to v and v is not an integer, then the following series approximation can be used for Yv(x), this is also an area where other approximations are often too slow to converge to be used (see http://functions.wolfram.com/03.03.06.0034.01):

When x is small compared to v, Jvx is best computed directly from the series:

In the general case we compute Jv and Yv simultaneously.
To get the initial values, let μ = ν - floor(ν + 1/2), then μ is the fractional part of ν such that |μ| <= 1/2 (we need this for convergence later). The idea is to calculate Jμ(x), Jμ+1(x), Yμ(x), Yμ+1(x) and use them to obtain Jν(x), Yν(x).
The algorithm is called Steed's method, which needs two continued fractions as well as the Wronskian:


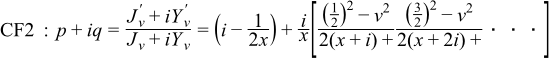
See: F.S. Acton, Numerical Methods that Work, The Mathematical Association of America, Washington, 1997.
The continued fractions are computed using the modified Lentz's method (W.J. Lentz, Generating Bessel functions in Mie scattering calculations using continued fractions, Applied Optics, vol 15, 668 (1976)). Their convergence rates depend on x, therefore we need different strategies for large x and small x.
x > v, CF1 needs O(x) iterations to converge, CF2 converges rapidly
x <= v, CF1 converges rapidly, CF2 fails to converge
when x -> 0
When x is large (x > 2), both continued fractions converge (CF1 may be slow for really large x). Jμ, Jμ+1, Yμ, Yμ+1 can be calculated by

where

Jν and Yμ are then calculated using backward (Miller's algorithm) and forward recurrence respectively.
When x is small (x <= 2), CF2 convergence may fail (but CF1 works very well). The solution here is Temme's series:

where

gk and hk are also computed by recursions (involving gamma functions), but the formulas are a little complicated, readers are refered to N.M. Temme, On the numerical evaluation of the ordinary Bessel function of the second kind, Journal of Computational Physics, vol 21, 343 (1976). Note Temme's series converge only for |μ| <= 1/2.
As the previous case, Yν is calculated from the forward recurrence, so is Yν+1. With these two values and fν, the Wronskian yields Jν(x) directly without backward recurrence.