 Boost
C++ Libraries
Boost
C++ Libraries
...one of the most highly
regarded and expertly designed C++ library projects in the
world.
— Herb Sutter and Andrei
Alexandrescu, C++
Coding Standards
 Boost
C++ Libraries
Boost
C++ Libraries
...one of the most highly
regarded and expertly designed C++ library projects in the
world.
— Herb Sutter and Andrei
Alexandrescu, C++
Coding Standards
#include <boost/math/special_functions/gamma.hpp>
namespace boost{ namespace math{ template <class T1, class T2> calculated-result-type gamma_p(T1 a, T2 z); template <class T1, class T2, class Policy> calculated-result-type gamma_p(T1 a, T2 z, const Policy&); template <class T1, class T2> calculated-result-type gamma_q(T1 a, T2 z); template <class T1, class T2, class Policy> calculated-result-type gamma_q(T1 a, T2 z, const Policy&); template <class T1, class T2> calculated-result-type tgamma_lower(T1 a, T2 z); template <class T1, class T2, class Policy> calculated-result-type tgamma_lower(T1 a, T2 z, const Policy&); template <class T1, class T2> calculated-result-type tgamma(T1 a, T2 z); template <class T1, class T2, class Policy> calculated-result-type tgamma(T1 a, T2 z, const Policy&); }} // namespaces
There are four incomplete gamma functions: two are normalised versions (also known as regularized incomplete gamma functions) that return values in the range [0, 1], and two are non-normalised and return values in the range [0, Γ(a)]. Users interested in statistical applications should use the normalised versions (gamma_p and gamma_q).
All of these functions require a > 0 and z >= 0, otherwise they return the result of domain_error.
The final Policy argument is optional and can be used to control the behaviour of the function: how it handles errors, what level of precision to use etc. Refer to the policy documentation for more details.
The return type of these functions is computed using the result type calculation rules when T1 and T2 are different types, otherwise the return type is simply T1.
template <class T1, class T2> calculated-result-type gamma_p(T1 a, T2 z); template <class T1, class T2, class Policy> calculated-result-type gamma_p(T1 a, T2 z, const Policy&);
Returns the normalised lower incomplete gamma function of a and z:

This function changes rapidly from 0 to 1 around the point z == a:

template <class T1, class T2> calculated-result-type gamma_q(T1 a, T2 z); template <class T1, class T2, class Policy> calculated-result-type gamma_q(T1 a, T2 z, const Policy&);
Returns the normalised upper incomplete gamma function of a and z:

This function changes rapidly from 1 to 0 around the point z == a:

template <class T1, class T2> calculated-result-type tgamma_lower(T1 a, T2 z); template <class T1, class T2, class Policy> calculated-result-type tgamma_lower(T1 a, T2 z, const Policy&);
Returns the full (non-normalised) lower incomplete gamma function of a and z:

template <class T1, class T2> calculated-result-type tgamma(T1 a, T2 z); template <class T1, class T2, class Policy> calculated-result-type tgamma(T1 a, T2 z, const Policy&);
Returns the full (non-normalised) upper incomplete gamma function of a and z:
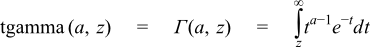
The following tables give peak and mean relative errors in over various domains of a and z, along with comparisons to the GSL-1.9 and Cephes libraries. Note that only results for the widest floating point type on the system are given as narrower types have effectively zero error.
Note that errors grow as a grows larger.
Note also that the higher error rates for the 80 and 128 bit long double results are somewhat misleading: expected results that are zero at 64-bit double precision may be non-zero - but exceptionally small - with the larger exponent range of a long double. These results therefore reflect the more extreme nature of the tests conducted for these types.
All values are in units of epsilon.
Table 3.3. Errors In the Function gamma_p(a,z)
|
Significand Size |
Platform and Compiler |
0.5 < a < 100 and 0.01*a < z < 100*a |
1x10-12 < a < 5x10-2 and 0.01*a < z < 100*a |
1e-6 < a < 1.7x106 and 1 < z < 100*a |
|---|---|---|---|---|
|
53 |
Win32, Visual C++ 8 |
Peak=36 Mean=9.1 (GSL Peak=342 Mean=46) (Cephes Peak=491 Mean=102) |
Peak=4.5 Mean=1.4 (GSL Peak=4.8 Mean=0.76) (Cephes Peak=21 Mean=5.6) |
Peak=244 Mean=21 (GSL Peak=1022 Mean=1054) (Cephes Peak~8x106 Mean~7x104) |
|
64 |
RedHat Linux IA32, gcc-3.3 |
Peak=241 Mean=36 |
Peak=4.7 Mean=1.5 |
Peak~30,220 Mean=1929 |
|
64 |
Redhat Linux IA64, gcc-3.4 |
Peak=41 Mean=10 |
Peak=4.7 Mean=1.4 |
Peak~30,790 Mean=1864 |
|
113 |
HPUX IA64, aCC A.06.06 |
Peak=40.2 Mean=10.2 |
Peak=5 Mean=1.6 |
Peak=5,476 Mean=440 |
Table 3.4. Errors In the Function gamma_q(a,z)
|
Significand Size |
Platform and Compiler |
0.5 < a < 100 and 0.01*a < z < 100*a |
1x10-12 < a < 5x10-2 and 0.01*a < z < 100*a |
1x10-6 < a < 1.7x106 and 1 < z < 100*a |
|---|---|---|---|---|
|
53 |
Win32, Visual C++ 8 |
Peak=28.3 Mean=7.2 (GSL Peak=201 Mean=13) (Cephes Peak=556 Mean=97) |
Peak=4.8 Mean=1.6 (GSL Peak~1.3x1010 Mean=1x10+9) (Cephes Peak~3x1011 Mean=4x1010) |
Peak=469 Mean=33 (GSL Peak=27,050 Mean=2159) (Cephes Peak~8x106 Mean~7x105) |
|
64 |
RedHat Linux IA32, gcc-3.3 |
Peak=280 Mean=33 |
Peak=4.1 Mean=1.6 |
Peak=11,490 Mean=732 |
|
64 |
Redhat Linux IA64, gcc-3.4 |
Peak=32 Mean=9.4 |
Peak=4.7 Mean=1.5 |
Peak=6815 Mean=414 |
|
113 |
HPUX IA64, aCC A.06.06 |
Peak=37 Mean=10 |
Peak=11.2 Mean=2.0 |
Peak=4,999 Mean=298 |
Table 3.5. Errors In the Function tgamma_lower(a,z)
|
Significand Size |
Platform and Compiler |
0.5 < a < 100 and 0.01*a < z < 100*a |
1x10-12 < a < 5x10-2 and 0.01*a < z < 100*a |
|---|---|---|---|
|
53 |
Win32, Visual C++ 8 |
Peak=5.5 Mean=1.4 |
Peak=3.6 Mean=0.78 |
|
64 |
RedHat Linux IA32, gcc-3.3 |
Peak=402 Mean=79 |
Peak=3.4 Mean=0.8 |
|
64 |
Redhat Linux IA64, gcc-3.4 |
Peak=6.8 Mean=1.4 |
Peak=3.4 Mean=0.78 |
|
113 |
HPUX IA64, aCC A.06.06 |
Peak=6.1 Mean=1.8 |
Peak=3.7 Mean=0.89 |
Table 3.6. Errors In the Function tgamma(a,z)
|
Significand Size |
Platform and Compiler |
0.5 < a < 100 and 0.01*a < z < 100*a |
1x10-12 < a < 5x10-2 and 0.01*a < z < 100*a |
|---|---|---|---|
|
53 |
Win32, Visual C++ 8 |
Peak=5.9 Mean=1.5 |
Peak=1.8 Mean=0.6 |
|
64 |
RedHat Linux IA32, gcc-3.3 |
Peak=596 Mean=116 |
Peak=3.2 Mean=0.84 |
|
64 |
Redhat Linux IA64, gcc-3.4.4 |
Peak=40.2 Mean=2.5 |
Peak=3.2 Mean=0.8 |
|
113 |
HPUX IA64, aCC A.06.06 |
Peak=364 Mean=17.6 |
Peak=12.7 Mean=1.8 |
There are two sets of tests: spot tests compare values taken from Mathworld's online evaluator with this implementation to perform a basic "sanity check". Accuracy tests use data generated at very high precision (using NTL's RR class set at 1000-bit precision) using this implementation with a very high precision 60-term Lanczos approximation, and some but not all of the special case handling disabled. This is less than satisfactory: an independent method should really be used, but apparently a complete lack of such methods are available. We can't even use a deliberately naive implementation without special case handling since Legendre's continued fraction (see below) is unstable for small a and z.
These four functions share a common implementation since they are all related via:
1) 
2) 
3) 
The lower incomplete gamma is computed from its series representation:
4) 
Or by subtraction of the upper integral from either Γ(a) or 1 when x - (1(3x)) > a and x > 1.1/.
The upper integral is computed from Legendre's continued fraction representation:
5) 
When (x > 1.1) or by subtraction of the lower integral from either Γ(a) or 1 when x - (1(3x)) < a/.
For x < 1.1 computation of the upper integral is more complex as the continued fraction representation is unstable in this area. However there is another series representation for the lower integral:
6) 
That lends itself to calculation of the upper integral via rearrangement to:
7) 
Refer to the documentation for powm1 and tgamma1pm1 for details of their implementation. Note however that the precision of tgamma1pm1 is capped to either around 35 digits, or to that of the Lanczos approximation associated with type T - if there is one - whichever of the two is the greater. That therefore imposes a similar limit on the precision of this function in this region.
For x < 1.1 the crossover point where the result is ~0.5 no longer occurs for x ~ y. Using x * 0.75 < a as the crossover criterion for 0.5 < x <= 1.1 keeps the maximum value computed (whether it's the upper or lower interval) to around 0.75. Likewise for x <= 0.5 then using -0.4 / log(x) < a as the crossover criterion keeps the maximum value computed to around 0.7 (whether it's the upper or lower interval).
There are two special cases used when a is an integer or half integer, and the crossover conditions listed above indicate that we should compute the upper integral Q. If a is an integer in the range 1 <= a < 30 then the following finite sum is used:
9) 
While for half integers in the range 0.5 <= a < 30 then the following finite sum is used:
10) 
These are both more stable and more efficient than the continued fraction alternative.
When the argument a is large, and x ~ a then the series (4) and continued fraction (5) above are very slow to converge. In this area an expansion due to Temme is used:
11) 
12) 
13) 
14) 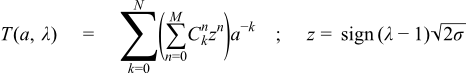
The double sum is truncated to a fixed number of terms - to give a specific target precision - and evaluated as a polynomial-of-polynomials. There are versions for up to 128-bit long double precision: types requiring greater precision than that do not use these expansions. The coefficients Ckn are computed in advance using the recurrence relations given by Temme. The zone where these expansions are used is
(a > 20) && (a < 200) && fabs(x-a)/a < 0.4
And:
(a > 200) && (fabs(x-a)/a < 4.5/sqrt(a))
The latter range is valid for all types up to 128-bit long doubles, and is
designed to ensure that the result is larger than 10-6, the first range is
used only for types up to 80-bit long doubles. These domains are narrower
than the ones recommended by either Temme or Didonato and Morris. However,
using a wider range results in large and inexact (i.e. computed) values being
passed to the exp and erfc functions resulting in significantly
larger error rates. In other words there is a fine trade off here between
efficiency and error. The current limits should keep the number of terms
required by (4) and (5) to no more than ~20 at double precision.
For the normalised incomplete gamma functions, calculation of the leading power terms is central to the accuracy of the function. For smallish a and x combining the power terms with the Lanczos approximation gives the greatest accuracy:
15) 
In the event that this causes underflow/overflow then the exponent can be reduced by a factor of a and brought inside the power term.
When a and x are large, we end up with a very large exponent with a base near one: this will not be computed accurately via the pow function, and taking logs simply leads to cancellation errors. The worst of the errors can be avoided by using:
16) 
when a-x is small and a and x are large. There is still a subtraction and therefore some cancellation errors - but the terms are small so the absolute error will be small - and it is absolute rather than relative error that counts in the argument to the exp function. Note that for sufficiently large a and x the errors will still get you eventually, although this does delay the inevitable much longer than other methods. Use of log(1+x)-x here is inspired by Temme (see references below).