 Boost
C++ Libraries
Boost
C++ Libraries
...one of the most highly
regarded and expertly designed C++ library projects in the
world.
— Herb Sutter and Andrei
Alexandrescu, C++
Coding Standards
 Boost
C++ Libraries
Boost
C++ Libraries
...one of the most highly
regarded and expertly designed C++ library projects in the
world.
— Herb Sutter and Andrei
Alexandrescu, C++
Coding Standards
What are expression templates anyway? In short, expression templates are templates that you write to capture expressions so that they can be transformed and/or evaluated lazily.
An example of normal C++ expression is:
std::sqrt(3.0) + 8.0f
The compiler sees this and creates some representation of that expression inside the compiler. This is typically an abstract syntax tree (AST). The AST for the expression above might be:
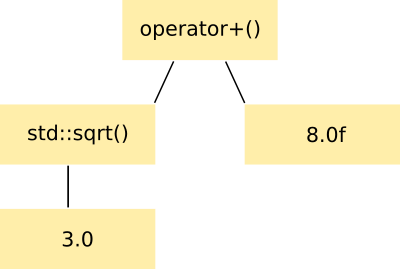
This tree structure captures all the elements of the original C++ code. The
expression is a plus operation whose left side is a call to std::sqrt(3.0)
and whose right side is 8.0f.
The call to std::sqrt(3.0) is its own expression subtree consisting
of a call node and its argument node.
A Boost.YAP version of this same tree is:
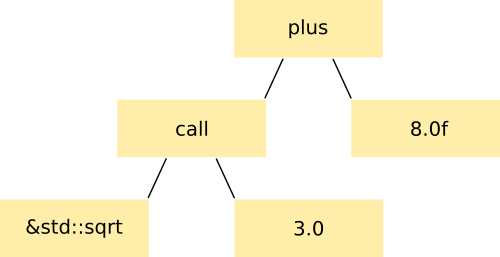
The operator+()
is represented by a Boost.YAP expression whose kind is yap::expr_kind::plus
and the call is represented by a Boost.YAP expression whose kind is yap::expr_kind::call.
Notice that the call expression has two terminals, one for the callable,
and one for its single argument.
The type that holds this expression is:
boost::yap::expression< boost::yap::expr_kind::plus, boost::hana::tuple< boost::yap::expression< boost::yap::expr_kind::call, boost::hana::tuple< boost::yap::expression< boost::yap::expr_kind::terminal, boost::hana::tuple<double (*)(double)> >, boost::yap::expression< boost::yap::expr_kind::terminal, boost::hana::tuple<double> > > >, boost::yap::expression< boost::yap::expr_kind::terminal, boost::hana::tuple<float> > > >
That looks like a big mess; let's unpack it. You might notice that the overall
shape is the same as the expression tree diagram above. We have tree-like
nesting of boost::yap::expression
template instantiations.
Here's the top-level boost::yap::expression again with its noisy guts removed:
boost::yap::expression< boost::yap::expr_kind::plus, boost::hana::tuple<
// Left and right operand expressions ...
> >
It has an expr_kind
of plus as its first template
parameter (it's a non-type parameter); this indicates what kind of "node"
it is. In this case, the top level expression is analogous to our operator+()
AST node. Its operands are the elements of its boost::hana::tuple<> data member.
The left operand to the top-level plus operation is itself a Boost.YAP expression
representing std::sqrt(3.0):
boost::yap::expression< boost::yap::expr_kind::call, boost::hana::tuple< boost::yap::expression< boost::yap::expr_kind::terminal, boost::hana::tuple<double (*)(double)> >, boost::yap::expression< boost::yap::expr_kind::terminal, boost::hana::tuple<double> > > >,
This expression is a call expression. The first operand to the call expression
is the callable entity, in this case a pointer to std::sqrt.
The remaining operands are the arguments to pass to the callable; in this
case, there's only one operand after the callable, 3.0.
The children of the std::sqrt(3.0) subexpression are terminals. This means
that they are leaf nodes in our notional AST.
The right operand to the top-level plus operation is of course also a Boost.YAP expression. It is also a terminal:
boost::yap::expression< boost::yap::expr_kind::terminal, boost::hana::tuple<float> >
Notice a couple of things here: 1) non-terminals (the top-level plus operation
and the call opertion in our example) have tuple elements that are all Boost.YAP expressions, and 2) terminals have tuple
elements, none of which are Boost.YAP expressions
(they're just normal types like float
and double (*)(double)).
![[Note]](../../../doc/src/images/note.png) |
Note |
|---|---|
From here on, I'll use the terms "expression" and "node" interchangably, and I'll also use the terms "subexpression" and "child" interchangably. Even though expression templates are not identical to tree-based ASTs, they're close enough that the terminology is interchangable without loss of meaning. |
If we want to capture an expression using Boost.YAP we have to do something
to let the compiler know not just to eagerly evaulate our expression, as
it does when it sees std::sqrt(3.0)
+ 8.0f.
To do this, we create expr_kind::terminal expressions out of one
or more of the terminals in the expression we want to capture and evaluate
lazily. Here, I've declared a template alias to make that easier to type:
template <typename T> using term = boost::yap::terminal<boost::yap::expression, T>;
And here is how I might use that alias to create the terminal containing
std::sqrt:
boost::yap::expression< boost::yap::expr_kind::plus, boost::hana::tuple< boost::yap::expression< boost::yap::expr_kind::call, boost::hana::tuple< boost::yap::expression< boost::yap::expr_kind::terminal, boost::hana::tuple<double (*)(double)> >, boost::yap::expression< boost::yap::expr_kind::terminal, boost::hana::tuple<double> > > >, boost::yap::expression< boost::yap::expr_kind::terminal, boost::hana::tuple<float> > > > yap_expr = term<double (*)(double)>{{std::sqrt}}(3.0) + 8.0f;
The reason I can then just call the terminal with a 3.0
argument and add 8.0f to the
result is that I'm taking a great big shortcut in this example by using Boost.YAP's
built-in example expression template, expression<>.
expression<> is a template with all
the operator overloads defined, including the call operator. Each operator
overload returns an expression<>,
which is why the + in std::sqrt(3.0)
+ 8.0f
also works.
![[Note]](../../../doc/src/images/note.png) |
Note |
|---|---|
|
(a + b) = c;
is at least unusual, if not outright wrong. Where does |
Boost.YAP comes with a handy print()
function. Calling it like this:
print(std::cout, yap_expr);
Gives this output:
expr<+> expr<()> term<double (*)(double)>[=1] term<double>[=3] term<float>[=8]
This is a lot more readable. I show this to you here to give you a more concise view of the AST-like structure.
(In case you're wondering why &std::sqrt
is printed as the value 1, so
was I. Apparently, that's just what GCC prints for that. Weird.)
Now we've seen a simple expression both described as a C++ AST and captured as a Boost.YAP expression. This just introduces the expression template mechanism; what do we do with it once we have an expression template? Consider one of the examples from the intro:
std::vector<int> v1 = {/* ... */}; std::vector<int> v2 = sort(v) | unique;
The rest of the tutorial will explain in greater detail how Boost.YAP can be used in situations like this, but the brief version is this:
auto expr
= sort(v) | unique;.
transform()
algorithm to transform the expression into what you want. In this case,
something like auto desired_expr
= yap::transform(expr, my_transform);, which turns the concise form sort(v) | unique
into the more verbose calls required by the standard algorithm APIs.
Note that the resulting expression can be transformed repeatedly if this
is desirable.
evaluate()
or a call to transform()
that transforms the final expression into an evaluated result.
There are certain idioms that Boost.YAP is written to support. Before getting into the nuts and bolts of how Boost.YAP operates, let's define these idioms.
evaluate(transform())
This is the main idiom you'll see reinforced in the examples. The idea is that you capture an expression:
auto expr_0 = /* ... */ ;
then transform it one or more times:
auto expr_1 = boost::yap::transform(expr_0, my_transform_1); auto expr_2 = boost::yap::transform(expr_1, my_transform_2); // ... auto expr_n = boost::yap::transform(expr_n_minus_1, my_transform_n);
and then finally you evaluate it:
auto const result = boost::yap::evaluate(expr_n);
Each call to transform() here produces a new Expression that can subsequently
be transformed. This is conceptually similar to what happens inside many
compilers. Capturing the expression is analogous to the compiler's parse;
the transformations are analogous to optimization passes; and the evaluation
is analogous to code generation.
This keeps the meaning of your code quite clear and easy to follow. For this reason, I think you should try to use Boost.YAP in this way when you can.
transform()-as-evaluate
This is a variant of evaluate(transform()), where the evaluate()
call at the end is unnecessary, because the final (or perhaps only) transform
does all the evaluation we need.
For instance, here is the get_arity
transform object used in the Calc3
example (don't worry too much about the implementation — we'll return
to this later in the docs in much greater detail):
struct get_arity { // Base case 1: Match a placeholder terminal, and return its arity as the // result. template <long long I> boost::hana::llong<I> operator() (boost::yap::expr_tag<boost::yap::expr_kind::terminal>, boost::yap::placeholder<I>) { return boost::hana::llong_c<I>; } // Base case 2: Match any other terminal. Return 0; non-placeholders do // not contribute to arity. template <typename T> auto operator() (boost::yap::expr_tag<boost::yap::expr_kind::terminal>, T &&) { using namespace boost::hana::literals; return 0_c; } // Recursive case: Match any expression not covered above, and return the // maximum of its children's arities. template <boost::yap::expr_kind Kind, typename... Arg> auto operator() (boost::yap::expr_tag<Kind>, Arg &&... arg) { return boost::hana::maximum( boost::hana::make_tuple( boost::yap::transform( boost::yap::as_expr(std::forward<Arg>(arg)), get_arity{} )... ) ); } };
Here is how this might be used:
auto expr = 1_p * 2_p; auto const arity = boost::yap::transform(expr, get_arity{}); static_assert(arity.value == 2, "Called with wrong number of args.");
In this case, transform() produces a non-Expression
value, all by itself. We got our result without ever needing to call evaluate().
![[Note]](../../../doc/src/images/note.png) |
Note |
|---|---|
Whether |
Boost.YAP consists of expressions and functions that operate on them. A function that takes an expression will accept any type that models the Expression concept.
For a type T to model the
Expression concept,
T must contain at least an
expr_kind
(terminal, plus-operation, etc.) and a boost::hana::tuple<> of values. That's it.
![[Note]](../../../doc/src/images/note.png) |
Note |
|---|---|
The |
Here's an example of an expression:
template <boost::yap::expr_kind Kind, typename Tuple> struct minimal_expr { static const boost::yap::expr_kind kind = Kind; Tuple elements; };
That's a template that models ExpressionTemplate. Instantiated with the proper template parameters, it produces Expressions.
Ok, so it's not that interesting by itself — minimal_expr
has no operations defined for it. But we can still use it with the Boost.YAP
functions that take an Expression.
Let's make a Boost.YAP plus-expression manually:
auto left = boost::yap::make_terminal<minimal_expr>(1); auto right = boost::yap::make_terminal<minimal_expr>(41); auto expr = boost::yap::make_expression< minimal_expr, boost::yap::expr_kind::plus >(left, right);
If we evaluate it using evaluate(),
it does what you would expect:
auto result = boost::yap::evaluate(expr); std::cout << result << "\n"; // prints "42"
One more thing. It is important to remember that Boost.YAP expressions are
all-lazy, all the time. There is no auto-evaluation of a Boost.YAP expression
like there is with normal C++ expressions. If you want your expressions to
be evaluated, you must call evaluate(),
or define non-lazy operations that force evaluation where and when you want
it. This last approach is usually the right one, and there are lots of examples
of how to do this in the Examples
section. In particular, checkout the Lazy
Vector and TArray
examples.
Because Boost.YAP operates on Expressions, it is possible to mix and match Expressions that are instantiations of different templates.
Here's why that's important. Say we have two types in a library. S is a string type, and M
is a matrix type. In the code here, s
and m are objects of types
S and M
respectively. Say we also have typical operator overloads for these types,
so m *
m and s[0]
are well-formed expressions, but m[0]
and s *
s are not.
To use these with Boost.YAP I might write an expression template for each:
template <...> struct m_expr { // ... }; BOOST_YAP_USER_BINARY_OPERATOR(times, m_expr, m_expr) template <...> struct s_expr { // ... BOOST_YAP_USER_SUBSCRIPT_OPERATOR(::s_expr) };
With this, I might write a Boost.YAP expression like:
some_expr_producing_func(S("my_matrix")) * some_matrix
I can transform this expression however I like, and do not have to worry about the fact that it contains expressions instantiated from different templates.
If Boost.YAP required an expression to be instantiated from a single expression
template expr<>,
expr<>
would have to have both operators. This means that all of a sudden s * s
and m[0] would be
well-formed expressions within a Boost.YAP expression, but not
for the real types S and
M respectively. That would
be super weird.
Most of the expression kinds are the overloadable operators (operator!(),
operator<<=(),
etc.), See expr_kind
for the full list.
There are three special kinds of expressions:
expr_kind::terminal
A terminal contains a non-Expression value, and represents a leaf-node
in an expression tree. A terminal may have a placeholder<>
value, in which case it acts as a placeholder.
expr_kind::if_else
An if_else expression
is analogous to the C++ ternary operator (?:).
It's up to you to make sure that the conditional expression given to
if_else can be converted
to bool; Boost.YAP does
not check this.
expr_kind::expr_ref
An expr_ref expression
is one that acts as a (possibly const)
lvalue reference to another expression. It exists to prevent unnecessary
copies of expressions.
Let's see an expression template type with some operators:
template <boost::yap::expr_kind Kind, typename Tuple> struct lazy_vector_expr { static const boost::yap::expr_kind kind = Kind; Tuple elements; // Note that this does not return an expression; it is greedily evaluated. auto operator[] (std::size_t n) const; }; BOOST_YAP_USER_BINARY_OPERATOR(plus, lazy_vector_expr, lazy_vector_expr) BOOST_YAP_USER_BINARY_OPERATOR(minus, lazy_vector_expr, lazy_vector_expr)
Those macros are used to define operator overloads that return Expressions.
As shown here, that sort of operator can be mixed with normal, non-lazy ones
— the operator[]
is a normal eager function.
Use of the macros is not necessary (you can write your own operators that return Expressions if you like), but it is suitable 99% of the time.
Making the operators easy to define like this allows you to define custom expression templates that have only the operators defined that are appropriate for your use case.
Detailed documentation on all the available macros can be found later in the Operator Macros section.
Transformations in Boost.YAP are done using the transform()
function.
Let's take another look at the example expression from the intro:

Consider a call to transform(),
operating on that expression:
auto result = boost::yap::transform(expr, xform);
Boost.YAP's transform() first looks at the top level
expression, which in this case is a +
expression. If the transform object xform
matches the + expression, transform() is done; it just returns
xform(expr).
If xform does not match the
+ expression, transform() transforms all its operands
(which for operator+()
is just the left and right operands), and returns a new +
expression with those transformed operands. What I mean by "match"
is covered in detail below.
The overall effect of this is that transform()
effectively copies an expr
node that does not match xform,
and returns a transformed node for an expr
node that does match xform.
transform() can also take multiple transform
objects. If you call it with N transform objects, it will attempt to match
each of the N transforms to a given expression, one at a time and in their
given order. Only if no transform matches an expression does the copy-and-recurse
behavior kick in.
![[Note]](../../../doc/src/images/note.png) |
Note |
|---|---|
There's another form of |
One common result of calling transform()
is that you create a copy of expr,
with a few matching nodes transformed. But this does not have to be the result
of calling transform(), because a Boost.YAP transformation
is free-form; it must return a value, but may do just about anything else.
It can transform an expression into anything — a new expression of
any kind, or even a non-expression value (effectively evaluating the expression).
As before, here is the get_arity
transform from the Calc3
example. It returns a value, not an Expression:
struct get_arity { // Base case 1: Match a placeholder terminal, and return its arity as the // result. template <long long I> boost::hana::llong<I> operator() (boost::yap::expr_tag<boost::yap::expr_kind::terminal>, boost::yap::placeholder<I>) { return boost::hana::llong_c<I>; } // Base case 2: Match any other terminal. Return 0; non-placeholders do // not contribute to arity. template <typename T> auto operator() (boost::yap::expr_tag<boost::yap::expr_kind::terminal>, T &&) { using namespace boost::hana::literals; return 0_c; } // Recursive case: Match any expression not covered above, and return the // maximum of its children's arities. template <boost::yap::expr_kind Kind, typename... Arg> auto operator() (boost::yap::expr_tag<Kind>, Arg &&... arg) { return boost::hana::maximum( boost::hana::make_tuple( boost::yap::transform( boost::yap::as_expr(std::forward<Arg>(arg)), get_arity{} )... ) ); } };
Also, note that in this case the transform is stateless, but you could also give your transform objects data members containing contextual state:
struct take_nth { template <typename T> auto operator() (boost::yap::expr_tag<boost::yap::expr_kind::terminal>, std::vector<T> const & vec) { return boost::yap::make_terminal(vec[n]); } std::size_t n; };
![[Tip]](../../../doc/src/images/tip.png) |
Tip |
|---|---|
Often when you create an expression, you will want to evaluate it in different
contexts, changing its evaluation — or even entire meaning —
in each context. |
As described above, transform()
only recurses when it does not find a match.
This means that if you want to transform a nonterminal, say an expr_kind::call expression we'll call C, and also
C's subexpressions, you must
explicitly call transform() yourself in your transform
that matches C. You can see
this kind of explicit transform()
call in the recursive case of get_arity
in the example code above.
![[Note]](../../../doc/src/images/note.png) |
Note |
|---|---|
The code you write with Boost.YAP is likely going to be very generic, especially
when you're writing a transform. |
In Boost.YAP a Transform is a Callable that has zero or more overloads that model the ExpressionTransform or TagTransform concepts.
An ExpressionTransform overload takes a single parameter whose type is the expression to be transformed. Here's one from a transform object in the Future Group example:
// Transform left || right -> transform(left). template <typename T, typename U> auto operator() ( future_expr< boost::yap::expr_kind::logical_or, boost::hana::tuple<T, U> > const & or_expr ) { // Recursively transform the left side, and return the result. // Without the recursion, we might return a terminal expression here // insead of a tuple. return boost::yap::transform(boost::yap::left(or_expr), *this); }
ExpressionTransforms
are most useful when you want to transform a narrow set of expression types
(perhaps only one). In particular, you can distinguish between const and non-const,
reference and non-reference, etc., in the expression and its operands in
a way that you have less control over with the other kind of transform.
A TagTransform overload
takes a tag that indicates the expr_kind of the expression
to be transformed, and then (loosely) the value of each operand of the expression
to be transformed. This looseness prevents you from needing to write out
the full type of the matched expression. Here's one from the Pipable
Algorithms example:
template<typename Range> auto operator()( boost::yap::expr_tag<boost::yap::expr_kind::call>, algorithm_t a, Range & r) { return call_algorithm(a, r); }
TagTransforms are
most useful when the transform needs to match an expression without regard
to whether its operands are expr_kind::expr_ref expressions, or —
if they are terminals — whether they contain or refer to their values.
TagTransforms tend
to be far more concise.
That "(loosely)" before probably bothered you, right? Me too. Each
non-tag parameter is passed to a TagTransform
by calling an operand accessor appropriate to expr's
kind, and then calling a terminal-specific version of value()
(terminal_value())
on the result. For example, consider a plus expression expr.
The TagTransform on
a transform object xform
would be called like this:
xform(plus_tag, terminal_value(left(expr)), terminal_value(right(expr)))
The operand accessors (left()
and right() in this example) all dereference
expr_kind::expr_ref
expressions before operating on them, and terminal_value() does the same.
terminal_value()
works much like value(), except that it does not
take the value of a nonterminal unary expression;
it just forwards a nonterminal through. It still takes values out of terminals
and unwraps expr_kind::expr_ref
expressions, though.
The auto-unwrapping of terminals means that you can effectively ignore the
presence of expr_kind::expr_ref
expressions when writing a TagTransform.
You can also just deal with the values inside terminals, and not the terminals
themselves. Also, you can match all terminal value qualifiers (const or not, lvalue or rvalue) uniformly
with a T const
& parameter. Finally, you can
write TagTransform
parameter types that can catch conversions; for instance, you can match any
negation expression containing a terminal, or a reference
to one, containing a value convertible to double
like this:
struct xform { auto operator() (boost::yap::negate_tag, double x) { return /* ... */; } }
That will match a negation of a terminal containing an unsigned
int, unsigned
int &,
int const
&, float
&&, etc. It will also match
a negation of a reference to such a terminal.
You can have two overloads in your transform that match an expression, one an ExpressionTransform and one a TagTransform, and there will not be any ambiguity. The TagTransform is matched first, and the ExpressionTransform is matched only if the TagTransform did not. You don't have to worry about ambiguity, but save yourself some confusion and mix the two kinds of overloads as little as possible.
![[Note]](../../../doc/src/images/note.png) |
Note |
|---|---|
The above only applies when you have an ExpressionTransform and a TagTransform that match the same kind of expression. Having unrelated ExpressionTransforms and TagTransforms within the same transform object is often quite useful. |
In the case that multiple transform objects are being used in transform(), the above logic applies
to each one independently before the next one is used. In other words, in
the call boost::yap::transform(expr,
a, b), transform() tries to match any TagTransform from a to an expression first, then any ExpressionTransform
from a, then any TagTransform
from b, and finally any
ExpressionTransform
from b. Only the first matching
overload in this sequence is used; all overloads later in the sequence or
in later transforms, whether they match or not, are simply ignored.
Boost.YAP comes with a couple of functions that return ready-made transforms,
replacements() and evaluation().
The transforms returned by replacements()
replace only placeholder terminals. Placeholder I
is replaced by the I-1-th argument passed to replacements().
Placeholders are 1-based for
consistency with other Boost and std
placeholders.
There are also a couple of specialty transform functions, replace_placeholders()
and evaluate(). These are convenience functions
that just call transform() on an expression using
replacements() or evaluation()
as the transform, respectively.
The behavior of evaluation()
is covered in the next section, Evaluating
Expressions.
Boost.YAP expressions are evaluated explicitly, by calling the evaluate() function or calling transform() using a transform object
returned from evaluation(). The former is a convenince
function that does the latter.
evaluate() simply removes all the Boost.YAP
machinery from an expression and evaluates it exactly as it would have been
if Boost.YAP were not used. This means that functions are called, operators
evaluated, etc. all as normal. To illustrate this, take a look at the implementation
of operator,()
used in evaluate():
template<typename T, typename U> constexpr decltype(auto) operator()(expr_tag<expr_kind::comma>, T && t, U && u) const { return transform( as_expr<minimal_expr>(static_cast<T &&>(t)), *this), transform( as_expr<minimal_expr>(static_cast<U &&>(u)), *this); }
What this transformation does is transform the left and right expressions,
and then use the built-in operator,() on the result. The evaluation transformations
for the other operators do the same thing — evaluate the operands,
then return the result of applying the built-in operator to the operands.
Function calls are done in a similar way, except that the callable is also a subexpression that needs to be evaluated before being called:
template<typename Callable, typename... Args> constexpr decltype(auto) operator()( expr_tag<expr_kind::call>, Callable && callable, Args &&... args) const { return transform(as_expr<minimal_expr>(static_cast<Callable &&>(callable)), *this)( transform(as_expr<minimal_expr>(static_cast<Args &&>(args)), *this)... ); }
If you got here without reading the Operators section, go read that first. Here are the operator macros and their uses:
Table 48.1. Unary and Binary Operator-Defining Macros
|
Macro |
Use |
First/Left Operand Type |
Right Operand Type |
Notes |
|---|---|---|---|---|
|
Unary operators. |
An Expression
instantiated from ExpressionTemplate
macro parameter |
-- |
||
|
Binary operators. |
Any type. |
Any type. |
At least one parameter must be an Expression
instantiated from ExpressionTemplate
macro parameter |
|
|
Free operators defined over non-Expression
types constrained by a type trait (e.g. all |
Any non-Expression that satisfies the given type trait. |
-- |
||
|
Free operators defined over non-Expression
types constrained by a pair of type traits (e.g. a |
Any non-Expression that satisfies the left-hand type trait. |
Any non-Expression that satisfies the right-hand type trait. |
||
|
Free operators defined over pairs of non-Expression
types, one constrained by a type trait and one not (e.g. a |
Any non-Expression. |
-- |
At least one parameter must satisfy the given type trait. |
Some operators may only be defined as member functions, and so are not covered by general-purpose the unary and binary operator macros above:
Table 48.2. The Member-Only Operator Macros
|
Macro |
Use |
Operands |
Notes |
|---|---|---|---|
|
Assignment operator. |
Any type except |
Does not conflict with the assignment or move assignment operators. |
|
|
Subscript operator. |
Any type. |
||
|
Call operator taking any number of parameters. |
Any type. |
||
|
Call operator taking exactly N parameters. |
Any type. |
Table 48.3. if_else Psuedo-Operator Macros
|
Macro |
Use |
Operands |
Notes |
|---|---|---|---|
|
Free |
Any type. |
At least one parameter must be an Expression. |
|
|
Free |
Any non-Expression. |
At least one parameter must satisfy the given type trait. |
![[Note]](../../../doc/src/images/note.png) |
Note |
|---|---|
Operands are handled in a uniform way across all functions defined by all the macros listed here. See How Expression Operands Are Treated for details. |
For any expression<> operator overload, or
any function defined using one of the function definition macros, operands
are treated in a uniform way.
The guiding design principle here is that an expression built using Boost.YAP should match the semantics of a builtin C++ expression as closely as possible. This implies that an rvalue be treated as if it were a temporary (as it may in fact have initially been) throughout the building and transformation of an expression, and that an lvalue should retain its connection to the underlying named entity to which it refers.
For example, if you see
auto expr = a + 1;
you should expect that a
will be an lvalue reference to some object of type decltype(a),
regardless of whether a is
a Boost.YAP Expression
or a builtin type. Similarly, you should expect the 1
to be an rvalue, whether wrapped in a terminal or not.
Let's take a quick look at make_terminal().
If you call it with a T rvalue,
the terminal's value type is a T,
and the rvalue gets moved into it. If you call it with a T
[const] lvalue, the value type is T [const] &, and
the reference refers to the lvalue (read [const] as
"possibly const-qualified").
This is important because you might write through the terminal later in an
assignment operation. You don't want to lose the ability to do this, or be
forced to write some Baroque pile of code to do so — it should be
natural and easy.
And it is:
int i = 0; auto expr = boost::yap::make_terminal(i) = 42; evaluate(expr); std::cout << i << "\n"; // Prints 42.
Now, there is a wrinkle. Boost.YAP's lazy expressions can be built piecemeal:
auto subexpr = boost::yap::make_terminal(1) + 2; // This is fine, and acts more-or-less as if you wrote "1 / (1 + 2)". auto expr = 1 / subexpr;
whereas C++'s eager builtin expressions cannot:
auto subexpr = 1 + 2; // Same as "int subexpr = 3;". Hm. auto expr = 1 / subexpr; // Same as "int expr = 0;" Arg.
Ok, so since you can build these lazy Boost.YAP expressions up from subexpressions,
how do we treat the subexpressions? We treat them in exactly the same way
as make_terminal() treats its parameter. Rvalues
are moved in, and lvalues are captured by (possibly const)
reference.
![[Note]](../../../doc/src/images/note.png) |
Note |
|---|---|
If you want to subvert the capture-by-reference semantics of using subexpressions,
just |
The capture-by-reference behavior is implemented via a special expr_kind,
expr_kind::expr_ref.
An expr_ref expression has
a single data element: a (possibly const
(Can I stop saying that every time? You get it, right? Ok, good.)) reference
to an expression. This additional level of indirection causes some complications
at times, as you can see in the examples. Fortunately, the complications
are not overly cumbersome.
So, given the rules above, here is a comprehensive breakdown of what happens
when an operand is passed to a Boost.YAP operator. In this table, expr_tmpl is an ExpressionTemplate,
and T is a non-Expression
type. E refers to any non-expr_ref Expression.
Boost.YAP does a partial decay on non-Expression
operands, in which cv and
reference qualifiers are left unchanged, but arrays are decayed to pointers
and functions are decayed to function pointers. PARTIAL_DECAY(T)
indicates such a partial decay of T.
Table 48.4. Operand Handling
|
Operand |
Captured As |
Notes |
|---|---|---|
|
|
|
|
|
|
|
|
|
|
|
Operand moved. |
|
|
|
|
|
|
|
|
|
|
|
Operand moved. |
|
|
|
|
|
|
|
|
|
|
|
Operand moved. |
The partial decay of non-Expression operands is another example of how Boost.YAP attempts to create expression trees that are as semantically close to builtin expressions as possible.
Boost.YAP has a convenient print()
function, that prints an expression tree to a stream. It is not intended
for production work (for instance, it has no formatting options), but it
is excellent for debugging and instrumentation.
Since it is only a debugging aid, print()
is found in a separate header not included when you include Boost.YAP with
#include <boost/yap/yap.hpp>
You must include <boost/yap/print.hpp>
explicitly.
print() handles several patterns
of expression specially, to allow a concise representation of a given expression
tree. For example, given this definition:
struct thing {};
and this expression:
using namespace boost::yap::literals; auto const const_lvalue_terminal_containing_rvalue = boost::yap::make_terminal("lvalue terminal"); double const d = 1.0; auto rvalue_terminal_containing_lvalue = boost::yap::make_terminal(d); auto thing_terminal = boost::yap::make_terminal(thing{}); auto expr = 4_p + std::move(rvalue_terminal_containing_lvalue) * thing_terminal - const_lvalue_terminal_containing_rvalue;
print() produces this output:
expr<->
expr<+>
term<boost::yap::placeholder<4ll>>[=4]
expr<*>
term<double &>[=1]
term<thing>[=<<unprintable-value>>] &
term<char const*>[=lvalue terminal] const &
As you can see, print() shows one node per line,
and represents the tree structure with indentation. It abbreviates non-terminal
nodes in the tree expr<op>,
where op is an operator symbol.
Terminal nodes are abbreviated term<T>,
where T is the type of value
contained in the terminal; this may be a reference type or a value.
A term node may not be a
terminal node at all, but an expr_kind::expr_ref expression containing a
terminal. Such a expr_kind::expr_ref node has a & or const
& suffix, to indicate that it
is a mutable or const reference,
respectively.
Each term node has a bracketed
value near the end. The format is [=X] where
X is the value the terminal
contains. If the terminal contains a value for which no operator<<(std::ostream &, ...)
overload exists (such as the thing
type above), X will be <<unprintable-value>>.
Most of these examples are patterned after the examples from Boost.Proto. In part, this was done to underscore where Boost.YAP can do what Proto can, and where it cannot.
Where possible, a Proto-derived example uses syntax in main() identical to that in the original Proto
example.
If you don't know anything about Proto, don't worry. The examples are useful on their own.
Remember how I mentioned earlier that Boost.YAP does things in a completely lazy way? Boost.YAP doesn't ever evaluate your expression eagerly. Eager evaluation can be done, but it's a bit of code.
#include <boost/yap/expression.hpp> #include <iostream> int main () { evaluate(boost::yap::make_terminal(std::cout) << "Hello" << ',' << " world!\n"); return 0; }
That's better! Sort of.... We created a custom expression template with an eager stream operator. This gives us eager evaluation, but gives away all the lazy AST building-then-evaluating that we're using expression templates for in the first place. In this simple example, we don't really need it.
#include <boost/yap/algorithm.hpp> #include <iostream> template <boost::yap::expr_kind Kind, typename Tuple> struct stream_expr { static const boost::yap::expr_kind kind = Kind; Tuple elements; template <typename T> decltype(auto) operator<< (T && x) { return boost::yap::value(*this) << std::forward<T &&>(x); } }; int main () { auto cout = boost::yap::make_terminal<stream_expr>(std::cout); cout << "Hello" << ',' << " world!\n"; return 0; }
minimal_expr below models
ExpressionTemplate;
since it has no operators, an expression must be built manually.
First, the template itself:
template <boost::yap::expr_kind Kind, typename Tuple> struct minimal_expr { static const boost::yap::expr_kind kind = Kind; Tuple elements; };
This can be used to make a minimal_expr
plus expression:
auto left = boost::yap::make_terminal<minimal_expr>(1); auto right = boost::yap::make_terminal<minimal_expr>(41); auto expr = boost::yap::make_expression< minimal_expr, boost::yap::expr_kind::plus >(left, right);
You can evaluate, transform, or otherwise operate on minimal_expr
expressions using the functions in Boost.YAP that accept an Expression:
auto result = boost::yap::evaluate(expr); std::cout << result << "\n"; // prints "42"
![[Note]](../../../doc/src/images/note.png) |
Note |
|---|---|
Don't use Boost.YAP this way. Use the operator macros instead. This is an example contrived only to show you the minimum requirements on a Boost.YAP-compatible template. |
This is the first of several calculator-building examples derived from Proto. This first one just builds lazy expressions with placeholders, and evaluates them. Here we can first see how much C++14-and-later language features help the end user — the Proto version is much, much longer.
#include <boost/yap/expression.hpp> #include <iostream> int main () { using namespace boost::yap::literals; // Displays "5" std::cout << evaluate( 1_p + 2.0, 3.0 ) << std::endl; // Displays "6" std::cout << evaluate( 1_p * 2_p, 3.0, 2.0 ) << std::endl; // Displays "0.5" std::cout << evaluate( (1_p - 2_p) / 2_p, 3.0, 2.0 ) << std::endl; return 0; }
The Proto Calc2 example turns the expressions from Calc1 into callable objects. Using Boost.YAP you can do this in two ways.
You can just use lambdas to wrap the expressions:
#include <boost/yap/expression.hpp> #include <iostream> int main () { using namespace boost::yap::literals; auto expr_1 = 1_p + 2.0; auto expr_1_fn = [expr_1](auto &&... args) { return evaluate(expr_1, args...); }; auto expr_2 = 1_p * 2_p; auto expr_2_fn = [expr_2](auto &&... args) { return evaluate(expr_2, args...); }; auto expr_3 = (1_p - 2_p) / 2_p; auto expr_3_fn = [expr_3](auto &&... args) { return evaluate(expr_3, args...); }; // Displays "5" std::cout << expr_1_fn(3.0) << std::endl; // Displays "6" std::cout << expr_2_fn(3.0, 2.0) << std::endl; // Displays "0.5" std::cout << expr_3_fn(3.0, 2.0) << std::endl; return 0; }
Or you can use make_expression_function()
to make a callable object from your expression:
#include <boost/yap/expression.hpp> #include <iostream> int main () { using namespace boost::yap::literals; // Displays "5" std::cout << make_expression_function(1_p + 2.0)(3.0) << std::endl; // Displays "6" std::cout << make_expression_function(1_p * 2_p)(3.0, 2.0) << std::endl; // Displays "0.5" std::cout << make_expression_function((1_p - 2_p) / 2_p)(3.0, 2.0) << std::endl; return 0; }
Here, we introduce a Transform
used to calculate expression arity, and static_assert() that the number of parameters passed
by the caller matches the arity.
![[Note]](../../../doc/src/images/note.png) |
Note |
|---|---|
The |
#include <boost/yap/expression.hpp> #include <boost/hana/maximum.hpp> #include <iostream> // Look! A transform! This one transforms the expression tree into the arity // of the expression, based on its placeholders. struct get_arity { // Base case 1: Match a placeholder terminal, and return its arity as the // result. template <long long I> boost::hana::llong<I> operator() (boost::yap::expr_tag<boost::yap::expr_kind::terminal>, boost::yap::placeholder<I>) { return boost::hana::llong_c<I>; } // Base case 2: Match any other terminal. Return 0; non-placeholders do // not contribute to arity. template <typename T> auto operator() (boost::yap::expr_tag<boost::yap::expr_kind::terminal>, T &&) { using namespace boost::hana::literals; return 0_c; } // Recursive case: Match any expression not covered above, and return the // maximum of its children's arities. template <boost::yap::expr_kind Kind, typename... Arg> auto operator() (boost::yap::expr_tag<Kind>, Arg &&... arg) { return boost::hana::maximum( boost::hana::make_tuple( boost::yap::transform( boost::yap::as_expr(std::forward<Arg>(arg)), get_arity{} )... ) ); } }; int main () { using namespace boost::yap::literals; // These lambdas wrap our expressions as callables, and allow us to check // the arity of each as we call it. auto expr_1 = 1_p + 2.0; auto expr_1_fn = [expr_1](auto &&... args) { auto const arity = boost::yap::transform(expr_1, get_arity{}); static_assert(arity.value == sizeof...(args), "Called with wrong number of args."); return evaluate(expr_1, args...); }; auto expr_2 = 1_p * 2_p; auto expr_2_fn = [expr_2](auto &&... args) { auto const arity = boost::yap::transform(expr_2, get_arity{}); static_assert(arity.value == sizeof...(args), "Called with wrong number of args."); return evaluate(expr_2, args...); }; auto expr_3 = (1_p - 2_p) / 2_p; auto expr_3_fn = [expr_3](auto &&... args) { auto const arity = boost::yap::transform(expr_3, get_arity{}); static_assert(arity.value == sizeof...(args), "Called with wrong number of args."); return evaluate(expr_3, args...); }; // Displays "5" std::cout << expr_1_fn(3.0) << std::endl; // Displays "6" std::cout << expr_2_fn(3.0, 2.0) << std::endl; // Displays "0.5" std::cout << expr_3_fn(3.0, 2.0) << std::endl; // Static-asserts with "Called with wrong number of args." //std::cout << expr_3_fn(3.0) << std::endl; // Static-asserts with "Called with wrong number of args." //std::cout << expr_3_fn(3.0, 2.0, 1.0) << std::endl; return 0; }
Finally, it starts to get interesting! This example shows how you can add plus and other operations to sequences of data without creating temporaries and allocating memory.
![[Note]](../../../doc/src/images/note.png) |
Note |
|---|---|
In this example, we see a terminal type that owns the storage of its
value, a |
#include <boost/yap/expression.hpp> #include <algorithm> #include <cassert> #include <iostream> #include <vector> template <boost::yap::expr_kind Kind, typename Tuple> struct lazy_vector_expr; // This transform turns a terminal of std::vector<double> into a terminal // containing the nth double in that vector. Think of it as turning our // expression of vectors into an expression of scalars. struct take_nth { boost::yap::terminal<lazy_vector_expr, double> operator() (boost::yap::terminal<lazy_vector_expr, std::vector<double>> const & expr); std::size_t n; }; // A custom expression template that defines lazy + and - operators that // produce expressions, and an eager [] operator that returns the nth element // of the expression. template <boost::yap::expr_kind Kind, typename Tuple> struct lazy_vector_expr { static const boost::yap::expr_kind kind = Kind; Tuple elements; // Note that this does not return an expression; it is greedily evaluated. auto operator[] (std::size_t n) const; }; BOOST_YAP_USER_BINARY_OPERATOR(plus, lazy_vector_expr, lazy_vector_expr) BOOST_YAP_USER_BINARY_OPERATOR(minus, lazy_vector_expr, lazy_vector_expr) template <boost::yap::expr_kind Kind, typename Tuple> auto lazy_vector_expr<Kind, Tuple>::operator[] (std::size_t n) const { return boost::yap::evaluate(boost::yap::transform(*this, take_nth{n})); } boost::yap::terminal<lazy_vector_expr, double> take_nth::operator() (boost::yap::terminal<lazy_vector_expr, std::vector<double>> const & expr) { double x = boost::yap::value(expr)[n]; // This move is something of a hack; we're forcing Yap to take a copy of x // by using std::move(). The move indicates that the terminal should keep // the value of x (since, being an rvalue, it may be a temporary), rather // than a reference to x. See the "How Expression Operands Are Treated" // section of the tutorial for details. return boost::yap::make_terminal<lazy_vector_expr, double>(std::move(x)); } // In order to define the += operator with the semantics we want, it's // convenient to derive a terminal type from a terminal instantiation of // lazy_vector_expr. Note that we could have written a template // specialization here instead -- either one would work. That would of course // have required more typing. struct lazy_vector : lazy_vector_expr< boost::yap::expr_kind::terminal, boost::hana::tuple<std::vector<double>> > { lazy_vector () {} explicit lazy_vector (std::vector<double> && vec) { elements = boost::hana::tuple<std::vector<double>>(std::move(vec)); } template <boost::yap::expr_kind Kind, typename Tuple> lazy_vector & operator+= (lazy_vector_expr<Kind, Tuple> const & rhs) { std::vector<double> & this_vec = boost::yap::value(*this); for (int i = 0, size = (int)this_vec.size(); i < size; ++i) { this_vec[i] += rhs[i]; } return *this; } }; int main () { lazy_vector v1{std::vector<double>(4, 1.0)}; lazy_vector v2{std::vector<double>(4, 2.0)}; lazy_vector v3{std::vector<double>(4, 3.0)}; double d1 = (v2 + v3)[2]; std::cout << d1 << "\n"; v1 += v2 - v3; std::cout << '{' << v1[0] << ',' << v1[1] << ',' << v1[2] << ',' << v1[3] << '}' << "\n"; // This expression is disallowed because it does not conform to the // implicit grammar. operator+= is only defined on terminals, not // arbitrary expressions. // (v2 + v3) += v1; return 0; }
In most of the examples, we've seen Boost.YAP expressions captured, transformed,
and/or evaluated either manually, or within certain operations that always
do certain transformations (as in the operator[] in the Lazy
Vector example).
Sometimes, you want the transfrmations to happen just before a Boost.YAP expression is used by non-Boost.YAP-aware code. At other times, you might want an entire Boost.YAP expression to be evaluated if it appears by itself in a statement (i.e. as an expression statement).
This example uses C++17's if constexpr (),
simply because it makes the example shorter and easier to digest. The
if constexpr
() bits are not strictly necessary.
#include <boost/yap/expression.hpp> #include <boost/optional.hpp> #include <boost/hana/fold.hpp> #include <boost/hana/maximum.hpp> #include <algorithm> #include <cassert> #include <iostream> #include <vector> // A super-basic matrix type, and a few associated operations. struct matrix { matrix() : values_(), rows_(0), cols_(0) {} matrix(int rows, int cols) : values_(rows * cols), rows_(rows), cols_(cols) { assert(0 < rows); assert(0 < cols); } int rows() const { return rows_; } int cols() const { return cols_; } double operator()(int r, int c) const { return values_[r * cols_ + c]; } double & operator()(int r, int c) { return values_[r * cols_ + c]; } private: std::vector<double> values_; int rows_; int cols_; }; matrix operator*(matrix const & lhs, double x) { matrix retval = lhs; for (int i = 0; i < retval.rows(); ++i) { for (int j = 0; j < retval.cols(); ++j) { retval(i, j) *= x; } } return retval; } matrix operator*(double x, matrix const & lhs) { return lhs * x; } matrix operator+(matrix const & lhs, matrix const & rhs) { assert(lhs.rows() == rhs.rows()); assert(lhs.cols() == rhs.cols()); matrix retval = lhs; for (int i = 0; i < retval.rows(); ++i) { for (int j = 0; j < retval.cols(); ++j) { retval(i, j) += rhs(i, j); } } return retval; } // daxpy() means Double-precision AX Plus Y. This crazy name comes from BLAS. // It is more efficient than a naive implementation, because it does not // create temporaries. The covnention of using Y as an out-parameter comes // from FORTRAN BLAS. matrix & daxpy(double a, matrix const & x, matrix & y) { assert(x.rows() == y.rows()); assert(x.cols() == y.cols()); for (int i = 0; i < y.rows(); ++i) { for (int j = 0; j < y.cols(); ++j) { y(i, j) += a * x(i, j); } } return y; } template <boost::yap::expr_kind Kind, typename Tuple> struct self_evaluating_expr; template <boost::yap::expr_kind Kind, typename Tuple> auto evaluate_matrix_expr(self_evaluating_expr<Kind, Tuple> const & expr); // This is the primary template for our expression template. If you assign a // self_evaluating_expr to a matrix, its conversion operator transforms and // evaluates the expression with a call to evaluate_matrix_expr(). template <boost::yap::expr_kind Kind, typename Tuple> struct self_evaluating_expr { operator auto() const; static const boost::yap::expr_kind kind = Kind; Tuple elements; }; // This is a specialization of our expression template for assignment // expressions. The destructor transforms and evaluates via a call to // evaluate_matrix_expr(), and then assigns the result to the variable on the // left side of the assignment. // // In a production implementation, you'd need to have specializations for // plus_assign, minus_assign, etc. template <typename Tuple> struct self_evaluating_expr<boost::yap::expr_kind::assign, Tuple> { ~self_evaluating_expr(); static const boost::yap::expr_kind kind = boost::yap::expr_kind::assign; Tuple elements; }; struct use_daxpy { // A plus-expression, which may be of the form double * matrix + matrix, // or may be something else. Since our daxpy() above requires a mutable // "y", we only need to match a mutable lvalue matrix reference here. template <typename Tuple> auto operator()( boost::yap::expr_tag<boost::yap::expr_kind::plus>, self_evaluating_expr<boost::yap::expr_kind::multiplies, Tuple> const & expr, matrix & m) { // Here, we transform the left-hand side into a pair if it's the // double * matrix operation we're looking for. Otherwise, we just // get a copy of the left side expression. // // Note that this is a bit of a cheat, done for clarity. If we pass a // larger expression that happens to contain a double * matrix // subexpression, that subexpression will be transformed into a tuple! // In production code, this transform should probably only be // performed on an expression with all terminal members. auto lhs = boost::yap::transform( expr, [](boost::yap::expr_tag<boost::yap::expr_kind::multiplies>, double d, matrix const & m) { return std::pair<double, matrix const &>(d, m); }); // If we got back a copy of expr above, just re-construct the // expression this function mathes; in other words, do not effectively // transform anything. Otherwise, replace the expression matched by // this function with a call to daxpy(). if constexpr (boost::yap::is_expr<decltype(lhs)>::value) { return expr + m; } else { return boost::yap::make_terminal(daxpy)(lhs.first, lhs.second, m); } } }; // This is the heart of what self_evaluating_expr does. If we had other // optimizations/transformations we wanted to do, we'd put them in this // function, either before or after the use_daxpy transformation. template <boost::yap::expr_kind Kind, typename Tuple> auto evaluate_matrix_expr(self_evaluating_expr<Kind, Tuple> const & expr) { auto daxpy_form = boost::yap::transform(expr, use_daxpy{}); return boost::yap::evaluate(daxpy_form); } template<boost::yap::expr_kind Kind, typename Tuple> self_evaluating_expr<Kind, Tuple>::operator auto() const { return evaluate_matrix_expr(*this); } template<typename Tuple> self_evaluating_expr<boost::yap::expr_kind::assign, Tuple>:: ~self_evaluating_expr() { using namespace boost::hana::literals; boost::yap::evaluate(elements[0_c]) = evaluate_matrix_expr(elements[1_c]); } // In order to define the = operator with the semantics we want, it's // convenient to derive a terminal type from a terminal instantiation of // self_evaluating_expr. Note that we could have written a template // specialization here instead -- either one would work. That would of course // have required more typing. struct self_evaluating : self_evaluating_expr< boost::yap::expr_kind::terminal, boost::hana::tuple<matrix> > { self_evaluating() {} explicit self_evaluating(matrix m) { elements = boost::hana::tuple<matrix>(std::move(m)); } BOOST_YAP_USER_ASSIGN_OPERATOR(self_evaluating_expr, ::self_evaluating_expr); }; BOOST_YAP_USER_BINARY_OPERATOR(plus, self_evaluating_expr, self_evaluating_expr) BOOST_YAP_USER_BINARY_OPERATOR(minus, self_evaluating_expr, self_evaluating_expr) BOOST_YAP_USER_BINARY_OPERATOR(multiplies, self_evaluating_expr, self_evaluating_expr) int main() { matrix identity(2, 2); identity(0, 0) = 1.0; identity(1, 1) = 1.0; // These are YAP-ified terminal expressions. self_evaluating m1(identity); self_evaluating m2(identity); self_evaluating m3(identity); // This transforms the YAP expression to use daxpy(), so it creates no // temporaries. The transform happens in the destructor of the // assignment-expression specialization of self_evaluating_expr. m1 = 3.0 * m2 + m3; // Same as above, except that it uses the matrix conversion operator on // the self_evaluating_expr primary template, because here we're assigning // a YAP expression to a non-YAP-ified matrix. matrix m_result_1 = 3.0 * m2 + m3; // Creates temporaries and does not use daxpy(), because the A * X + Y // pattern does not occur within the expression. matrix m_result_2 = 3.0 * m2; return 0; }
Proto refers to this as the "mini-library for linear algebra" example. It shows how quite complicated expressions involving sequences can be evaluated elementwise, requiring no temporaries.
![[Note]](../../../doc/src/images/note.png) |
Note |
|---|---|
The original Proto example used a terminal that contained an array of
three |
#include <boost/yap/algorithm.hpp> #include <boost/yap/print.hpp> #include <array> #include <iostream> template <boost::yap::expr_kind Kind, typename Tuple> struct tarray_expr; struct take_nth { boost::yap::terminal<tarray_expr, int> operator() (boost::yap::terminal<tarray_expr, std::array<int, 3>> const & expr); std::size_t n; }; // Another custom expression template. In this case, we static_assert() that // it only gets instantiated with terminals with pre-approved value types. template <boost::yap::expr_kind Kind, typename Tuple> struct tarray_expr { // Make sure that, if this expression is a terminal, its value is one we // want to support. Note that the presence of expr_kind::expr_ref makes // life slightly more difficult; we have to account for int const & and // int & as well as int. static_assert( Kind != boost::yap::expr_kind::terminal || std::is_same<Tuple, boost::hana::tuple<int const &>>{} || std::is_same<Tuple, boost::hana::tuple<int &>>{} || std::is_same<Tuple, boost::hana::tuple<int>>{} || std::is_same<Tuple, boost::hana::tuple<std::array<int, 3>>>{}, "tarray_expr instantiated with an unsupported terminal type." ); static const boost::yap::expr_kind kind = Kind; Tuple elements; int operator[] (std::size_t n) const { return boost::yap::evaluate(boost::yap::transform(*this, take_nth{n})); } }; // Define operators +, -, *, and /. BOOST_YAP_USER_BINARY_OPERATOR(plus, tarray_expr, tarray_expr) BOOST_YAP_USER_BINARY_OPERATOR(minus, tarray_expr, tarray_expr) BOOST_YAP_USER_BINARY_OPERATOR(multiplies, tarray_expr, tarray_expr) BOOST_YAP_USER_BINARY_OPERATOR(divides, tarray_expr, tarray_expr) boost::yap::terminal<tarray_expr, int> take_nth::operator() (boost::yap::terminal<tarray_expr, std::array<int, 3>> const & expr) { int x = boost::yap::value(expr)[n]; // Again, this is the move hack to get x into the resulting terminal as a // value instead of a reference. return boost::yap::make_terminal<tarray_expr>(std::move(x)); } // Stream-out operators for the two kinds of terminals we support. std::ostream & operator<< (std::ostream & os, boost::yap::terminal<tarray_expr, int> expr) { return os << '{' << boost::yap::value(expr) << '}'; } std::ostream & operator<< (std::ostream & os, boost::yap::terminal<tarray_expr, std::array<int, 3>> expr) { std::array<int, 3> const & a = boost::yap::value(expr); return os << '{' << a[0] << ", " << a[1] << ", " << a[2] << '}'; } // Stream-out operators for general expressions. Note that we have to treat // the reference case separately; this also could have been done using // constexpr if in a single function template. template <typename Tuple> std::ostream & operator<< (std::ostream & os, tarray_expr<boost::yap::expr_kind::expr_ref, Tuple> const & expr) { return os << boost::yap::deref(expr); } template <boost::yap::expr_kind Kind, typename Tuple> std::ostream & operator<< (std::ostream & os, tarray_expr<Kind, Tuple> const & expr) { if (Kind == boost::yap::expr_kind::plus || Kind == boost::yap::expr_kind::minus) os << '('; os << boost::yap::left(expr) << " " << op_string(Kind) << " " << boost::yap::right(expr); if (Kind == boost::yap::expr_kind::plus || Kind == boost::yap::expr_kind::minus) os << ')'; return os; } // Since we want different behavior on terminals than on other kinds of // expressions, we create a custom type that does so. struct tarray : tarray_expr< boost::yap::expr_kind::terminal, boost::hana::tuple<std::array<int, 3>> > { explicit tarray (int i = 0, int j = 0, int k = 0) { (*this)[0] = i; (*this)[1] = j; (*this)[2] = k; } explicit tarray (std::array<int, 3> a) { (*this)[0] = a[0]; (*this)[1] = a[1]; (*this)[2] = a[2]; } int & operator[] (std::ptrdiff_t i) { return boost::yap::value(*this)[i]; } int const & operator[] (std::ptrdiff_t i) const { return boost::yap::value(*this)[i]; } template <typename T> tarray & operator= (T const & t) { // We use as_expr() here to make sure that the value passed to // assign() is an expression. as_expr() simply forwards expressions // through, and wraps non-expressions as terminals. return assign(boost::yap::as_expr< ::tarray_expr>(t)); } template <typename Expr> tarray & printAssign (Expr const & expr) { *this = expr; std::cout << *this << " = " << expr << std::endl; return *this; } private: template <typename Expr> tarray & assign (Expr const & expr) { (*this)[0] = expr[0]; (*this)[1] = expr[1]; (*this)[2] = expr[2]; return *this; } }; int main() { tarray a(3,1,2); tarray b; std::cout << a << std::endl; std::cout << b << std::endl; b[0] = 7; b[1] = 33; b[2] = -99; tarray c(a); std::cout << c << std::endl; a = 0; std::cout << a << std::endl; std::cout << b << std::endl; std::cout << c << std::endl; a = b + c; std::cout << a << std::endl; a.printAssign(b+c*(b + 3*c)); return 0; }
An example using 3-space vectors, a bit like the tarray example.
#include <boost/yap/yap.hpp> #include <array> #include <iostream> struct take_nth { auto operator() (boost::yap::terminal<boost::yap::expression, std::array<int, 3>> const & expr) { int x = boost::yap::value(expr)[n]; // The move forces the terminal to store the value of x, not a // reference. return boost::yap::make_terminal(std::move(x)); } std::size_t n; }; // Since this example doesn't constrain the operators defined on its // expressions, we can just use boost::yap::expression<> as the expression // template. using vec3_terminal = boost::yap::expression< boost::yap::expr_kind::terminal, boost::hana::tuple<std::array<int, 3>> >; // Customize the terminal type we use by adding index and assignment // operations. struct vec3 : vec3_terminal { explicit vec3 (int i = 0, int j = 0, int k = 0) { (*this)[0] = i; (*this)[1] = j; (*this)[2] = k; } explicit vec3 (std::array<int, 3> a) { (*this)[0] = a[0]; (*this)[1] = a[1]; (*this)[2] = a[2]; } int & operator[] (std::ptrdiff_t i) { return boost::yap::value(*this)[i]; } int const & operator[] (std::ptrdiff_t i) const { return boost::yap::value(*this)[i]; } template <typename T> vec3 & operator= (T const & t) { decltype(auto) expr = boost::yap::as_expr(t); (*this)[0] = boost::yap::evaluate(boost::yap::transform(expr, take_nth{0})); (*this)[1] = boost::yap::evaluate(boost::yap::transform(expr, take_nth{1})); (*this)[2] = boost::yap::evaluate(boost::yap::transform(expr, take_nth{2})); return *this; } void print() const { std::cout << '{' << (*this)[0] << ", " << (*this)[1] << ", " << (*this)[2] << '}' << std::endl; } }; // This is a stateful transform that keeps a running count of the terminals it // has seen. struct count_leaves_impl { auto operator() (vec3_terminal const & expr) { value += 1; return expr; } int value = 0; }; template <typename Expr> int count_leaves (Expr const & expr) { count_leaves_impl impl; boost::yap::transform(boost::yap::as_expr(expr), impl); return impl.value; } int main() { vec3 a, b, c; c = 4; b[0] = -1; b[1] = -2; b[2] = -3; a = b + c; a.print(); vec3 d; auto expr1 = b + c; d = expr1; d.print(); int num = count_leaves(expr1); std::cout << num << std::endl; num = count_leaves(b + 3 * c); std::cout << num << std::endl; num = count_leaves(b + c * d); std::cout << num << std::endl; return 0; }
So far we've only seen examples with custom terminals that own the values
in the expressions we operate on. What happens when you've got types that
you want to operate on, non-intrusively? Here's how you might do it with
std::vector<>s:
#include <boost/yap/yap.hpp> #include <vector> #include <iostream> struct take_nth { template <typename T> auto operator() (boost::yap::expr_tag<boost::yap::expr_kind::terminal>, std::vector<T> const & vec) { return boost::yap::make_terminal(vec[n]); } std::size_t n; }; // A stateful transform that records whether all the std::vector<> terminals // it has seen are equal to the given size. struct equal_sizes_impl { template <typename T> auto operator() (boost::yap::expr_tag<boost::yap::expr_kind::terminal>, std::vector<T> const & vec) { auto const expr_size = vec.size(); if (expr_size != size) value = false; return 0; } std::size_t const size; bool value; }; template <typename Expr> bool equal_sizes (std::size_t size, Expr const & expr) { equal_sizes_impl impl{size, true}; boost::yap::transform(boost::yap::as_expr(expr), impl); return impl.value; } // Assigns some expression e to the given vector by evaluating e elementwise, // to avoid temporaries and allocations. template <typename T, typename Expr> std::vector<T> & assign (std::vector<T> & vec, Expr const & e) { decltype(auto) expr = boost::yap::as_expr(e); assert(equal_sizes(vec.size(), expr)); for (std::size_t i = 0, size = vec.size(); i < size; ++i) { vec[i] = boost::yap::evaluate( boost::yap::transform(boost::yap::as_expr(expr), take_nth{i})); } return vec; } // As assign() above, just using +=. template <typename T, typename Expr> std::vector<T> & operator+= (std::vector<T> & vec, Expr const & e) { decltype(auto) expr = boost::yap::as_expr(e); assert(equal_sizes(vec.size(), expr)); for (std::size_t i = 0, size = vec.size(); i < size; ++i) { vec[i] += boost::yap::evaluate( boost::yap::transform(boost::yap::as_expr(expr), take_nth{i})); } return vec; } // Define a type trait that identifies std::vectors. template <typename T> struct is_vector : std::false_type {}; template <typename T, typename A> struct is_vector<std::vector<T, A>> : std::true_type {}; // Define all the expression-returning numeric operators we need. Each will // accept any std::vector<> as any of its arguments, and then any value in the // remaining argument, if any -- some of the operators below are unary. BOOST_YAP_USER_UDT_UNARY_OPERATOR(negate, boost::yap::expression, is_vector); // - BOOST_YAP_USER_UDT_ANY_BINARY_OPERATOR(multiplies, boost::yap::expression, is_vector); // * BOOST_YAP_USER_UDT_ANY_BINARY_OPERATOR(divides, boost::yap::expression, is_vector); // / BOOST_YAP_USER_UDT_ANY_BINARY_OPERATOR(modulus, boost::yap::expression, is_vector); // % BOOST_YAP_USER_UDT_ANY_BINARY_OPERATOR(plus, boost::yap::expression, is_vector); // + BOOST_YAP_USER_UDT_ANY_BINARY_OPERATOR(minus, boost::yap::expression, is_vector); // - BOOST_YAP_USER_UDT_ANY_BINARY_OPERATOR(less, boost::yap::expression, is_vector); // < BOOST_YAP_USER_UDT_ANY_BINARY_OPERATOR(greater, boost::yap::expression, is_vector); // > BOOST_YAP_USER_UDT_ANY_BINARY_OPERATOR(less_equal, boost::yap::expression, is_vector); // <= BOOST_YAP_USER_UDT_ANY_BINARY_OPERATOR(greater_equal, boost::yap::expression, is_vector); // >= BOOST_YAP_USER_UDT_ANY_BINARY_OPERATOR(equal_to, boost::yap::expression, is_vector); // == BOOST_YAP_USER_UDT_ANY_BINARY_OPERATOR(not_equal_to, boost::yap::expression, is_vector); // != BOOST_YAP_USER_UDT_ANY_BINARY_OPERATOR(logical_or, boost::yap::expression, is_vector); // || BOOST_YAP_USER_UDT_ANY_BINARY_OPERATOR(logical_and, boost::yap::expression, is_vector); // && BOOST_YAP_USER_UDT_ANY_BINARY_OPERATOR(bitwise_and, boost::yap::expression, is_vector); // & BOOST_YAP_USER_UDT_ANY_BINARY_OPERATOR(bitwise_or, boost::yap::expression, is_vector); // | BOOST_YAP_USER_UDT_ANY_BINARY_OPERATOR(bitwise_xor, boost::yap::expression, is_vector); // ^ int main() { int i; int const n = 10; std::vector<int> a,b,c,d; std::vector<double> e(n); for (i = 0; i < n; ++i) { a.push_back(i); b.push_back(2*i); c.push_back(3*i); d.push_back(i); } // After this point, no allocations occur. assign(b, 2); assign(d, a + b * c); a += if_else(d < 30, b, c); assign(e, c); e += e - 4 / (c + 1); for (i = 0; i < n; ++i) { std::cout << " a(" << i << ") = " << a[i] << " b(" << i << ") = " << b[i] << " c(" << i << ") = " << c[i] << " d(" << i << ") = " << d[i] << " e(" << i << ") = " << e[i] << std::endl; } return 0; }
![[Note]](../../../doc/src/images/note.png) |
Note |
|---|---|
Though this example only provides overloads for the operations we want
to define over |
This is a lot like the previous Vector example, except that it operates
on std::vector<>s
and std::list<>s
in the same expression.
#include <boost/yap/yap.hpp> #include <complex> #include <list> #include <vector> #include <iostream> // This wrapper makes the pattern matching in transforms below (like deref and // incr) a lot easier to write. template <typename Iter> struct iter_wrapper { Iter it; }; template <typename Iter> auto make_iter_wrapper (Iter it) { return iter_wrapper<Iter>{it}; } // A container -> wrapped-begin transform. struct begin { template <typename Cont> auto operator() (boost::yap::expr_tag<boost::yap::expr_kind::terminal>, Cont const & cont) -> decltype(boost::yap::make_terminal(make_iter_wrapper(cont.begin()))) { return boost::yap::make_terminal(make_iter_wrapper(cont.begin())); } }; // A wrapped-iterator -> dereferenced value transform. struct deref { template <typename Iter> auto operator() (boost::yap::expr_tag<boost::yap::expr_kind::terminal>, iter_wrapper<Iter> wrapper) -> decltype(boost::yap::make_terminal(*wrapper.it)) { return boost::yap::make_terminal(*wrapper.it); } }; // A wrapped-iterator increment transform, using side effects. struct incr { template <typename Iter> auto operator() (boost::yap::expr_tag<boost::yap::expr_kind::terminal>, iter_wrapper<Iter> & wrapper) -> decltype(boost::yap::make_terminal(wrapper.it)) { ++wrapper.it; // Since this transform is valuable for its side effects, and thus the // result of the transform is ignored, we could return anything here. return boost::yap::make_terminal(wrapper.it); } }; // The implementation of elementwise evaluation of expressions of sequences; // all the later operations use this one. template < template <class, class> class Cont, typename T, typename A, typename Expr, typename Op > Cont<T, A> & op_assign (Cont<T, A> & cont, Expr const & e, Op && op) { decltype(auto) expr = boost::yap::as_expr(e); // Transform the expression of sequences into an expression of // begin-iterators. auto expr2 = boost::yap::transform(boost::yap::as_expr(expr), begin{}); for (auto && x : cont) { // Transform the expression of iterators into an expression of // pointed-to-values, evaluate the resulting expression, and call op() // with the result of the evaluation. op(x, boost::yap::evaluate(boost::yap::transform(expr2, deref{}))); // Transform the expression of iterators into an ignored value; as a // side effect, increment the iterators in the expression. boost::yap::transform(expr2, incr{}); } return cont; } template < template <class, class> class Cont, typename T, typename A, typename Expr > Cont<T, A> & assign (Cont<T, A> & cont, Expr const & expr) { return op_assign(cont, expr, [](auto & cont_value, auto && expr_value) { cont_value = std::forward<decltype(expr_value)>(expr_value); }); } template < template <class, class> class Cont, typename T, typename A, typename Expr > Cont<T, A> & operator+= (Cont<T, A> & cont, Expr const & expr) { return op_assign(cont, expr, [](auto & cont_value, auto && expr_value) { cont_value += std::forward<decltype(expr_value)>(expr_value); }); } template < template <class, class> class Cont, typename T, typename A, typename Expr > Cont<T, A> & operator-= (Cont<T, A> & cont, Expr const & expr) { return op_assign(cont, expr, [](auto & cont_value, auto && expr_value) { cont_value -= std::forward<decltype(expr_value)>(expr_value); }); } // A type trait that identifies std::vectors and std::lists. template <typename T> struct is_mixed : std::false_type {}; template <typename T, typename A> struct is_mixed<std::vector<T, A>> : std::true_type {}; template <typename T, typename A> struct is_mixed<std::list<T, A>> : std::true_type {}; // Define expression-producing operators over std::vectors and std::lists. BOOST_YAP_USER_UDT_UNARY_OPERATOR(negate, boost::yap::expression, is_mixed); // - BOOST_YAP_USER_UDT_ANY_BINARY_OPERATOR(multiplies, boost::yap::expression, is_mixed); // * BOOST_YAP_USER_UDT_ANY_BINARY_OPERATOR(divides, boost::yap::expression, is_mixed); // / BOOST_YAP_USER_UDT_ANY_BINARY_OPERATOR(modulus, boost::yap::expression, is_mixed); // % BOOST_YAP_USER_UDT_ANY_BINARY_OPERATOR(plus, boost::yap::expression, is_mixed); // + BOOST_YAP_USER_UDT_ANY_BINARY_OPERATOR(minus, boost::yap::expression, is_mixed); // - BOOST_YAP_USER_UDT_ANY_BINARY_OPERATOR(less, boost::yap::expression, is_mixed); // < BOOST_YAP_USER_UDT_ANY_BINARY_OPERATOR(greater, boost::yap::expression, is_mixed); // > BOOST_YAP_USER_UDT_ANY_BINARY_OPERATOR(less_equal, boost::yap::expression, is_mixed); // <= BOOST_YAP_USER_UDT_ANY_BINARY_OPERATOR(greater_equal, boost::yap::expression, is_mixed); // >= BOOST_YAP_USER_UDT_ANY_BINARY_OPERATOR(equal_to, boost::yap::expression, is_mixed); // == BOOST_YAP_USER_UDT_ANY_BINARY_OPERATOR(not_equal_to, boost::yap::expression, is_mixed); // != BOOST_YAP_USER_UDT_ANY_BINARY_OPERATOR(logical_or, boost::yap::expression, is_mixed); // || BOOST_YAP_USER_UDT_ANY_BINARY_OPERATOR(logical_and, boost::yap::expression, is_mixed); // && BOOST_YAP_USER_UDT_ANY_BINARY_OPERATOR(bitwise_and, boost::yap::expression, is_mixed); // & BOOST_YAP_USER_UDT_ANY_BINARY_OPERATOR(bitwise_or, boost::yap::expression, is_mixed); // | BOOST_YAP_USER_UDT_ANY_BINARY_OPERATOR(bitwise_xor, boost::yap::expression, is_mixed); // ^ // Define a type that can resolve to any overload of std::sin(). struct sin_t { template<typename T> T operator()(T x) { return std::sin(x); } }; int main() { int n = 10; std::vector<int> a,b,c,d; std::list<double> e; std::list<std::complex<double>> f; int i; for(i = 0;i < n; ++i) { a.push_back(i); b.push_back(2*i); c.push_back(3*i); d.push_back(i); e.push_back(0.0); f.push_back(std::complex<double>(1.0, 1.0)); } assign(b, 2); assign(d, a + b * c); a += if_else(d < 30, b, c); assign(e, c); e += e - 4 / (c + 1); auto sin = boost::yap::make_terminal(sin_t{}); f -= sin(0.1 * e * std::complex<double>(0.2, 1.2)); std::list<double>::const_iterator ei = e.begin(); std::list<std::complex<double>>::const_iterator fi = f.begin(); for (i = 0; i < n; ++i) { std::cout << "a(" << i << ") = " << a[i] << " b(" << i << ") = " << b[i] << " c(" << i << ") = " << c[i] << " d(" << i << ") = " << d[i] << " e(" << i << ") = " << *ei++ << " f(" << i << ") = " << *fi++ << std::endl; } return 0; }
An implementation of map_list_of() from Boost.Assign using Boost.YAP.
#include <boost/yap/algorithm.hpp> #include <map> #include <iostream> // This transform applies all the call-subexpressions in a map_list_of // expression (a nested chain of call operations) as a side effect; the // expression returned by the transform is ignored. template <typename Key, typename Value, typename Allocator> struct map_list_of_transform { template <typename Fn, typename Key2, typename Value2> auto operator() (boost::yap::expr_tag<boost::yap::expr_kind::call>, Fn const & fn, Key2 && key, Value2 && value) { // Recurse into the function subexpression. Remember, transform() // walks the nodes in an expression tree looking for matches. Once it // finds a match, it is finished with that matching subtree. So // without this recursive call, only the top-level call expression is // matched by transform(). boost::yap::transform( boost::yap::as_expr<boost::yap::minimal_expr>(fn), *this); map.emplace( std::forward<Key2 &&>(key), std::forward<Value2 &&>(value) ); // All we care about are the side effects of this transform, so we can // return any old thing here. return 0; } std::map<Key, Value, Allocator> & map; }; // A custom expression template type for map_list_of expressions. We only // need support for the call operator and an implicit conversion to a // std::map. template <boost::yap::expr_kind Kind, typename Tuple> struct map_list_of_expr { static boost::yap::expr_kind const kind = Kind; Tuple elements; template <typename Key, typename Value, typename Allocator> operator std::map<Key, Value, Allocator> () const { std::map<Key, Value, Allocator> retval; map_list_of_transform<Key, Value, Allocator> transform{retval}; boost::yap::transform(*this, transform); return retval; } BOOST_YAP_USER_CALL_OPERATOR_N(::map_list_of_expr, 2) }; // A tag type for creating the map_list_of function terminal. struct map_list_of_tag {}; auto map_list_of = boost::yap::make_terminal<map_list_of_expr>(map_list_of_tag{}); int main() { // Initialize a map: std::map<std::string, int> op = map_list_of ("<", 1) ("<=",2) (">", 3) (">=",4) ("=", 5) ("<>",6) ; std::cout << "\"<\" --> " << op["<"] << std::endl; std::cout << "\"<=\" --> " << op["<="] << std::endl; std::cout << "\">\" --> " << op[">"] << std::endl; std::cout << "\">=\" --> " << op[">="] << std::endl; std::cout << "\"=\" --> " << op["="] << std::endl; std::cout << "\"<>\" --> " << op["<>"] << std::endl; return 0; }
![[Note]](../../../doc/src/images/note.png) |
Note |
|---|---|
|
An implementation of Howard Hinnant's design for future groups.
#include <boost/yap/algorithm.hpp> #include <boost/hana/concat.hpp> // A custom expression template for future groups. It supports operators || // and &&. template <boost::yap::expr_kind Kind, typename Tuple> struct future_expr { static boost::yap::expr_kind const kind = Kind; future_expr (Tuple && tuple) : elements (std::forward<Tuple &&>(tuple)) {} Tuple elements; // Returns the transformed/flattened expression. auto get () const; }; BOOST_YAP_USER_BINARY_OPERATOR(logical_or, future_expr, future_expr) BOOST_YAP_USER_BINARY_OPERATOR(logical_and, future_expr, future_expr) // A special-cased future terminal that matches the semantics from the // original Proto example. template <typename T> struct future : future_expr<boost::yap::expr_kind::terminal, boost::hana::tuple<T>> { future (T const & t = T()) : future_expr<boost::yap::expr_kind::terminal, boost::hana::tuple<T>> (boost::hana::tuple<T>{t}) {} T get () const { return boost::yap::value(*this); } }; template <typename T> using remove_cv_ref_t = std::remove_cv_t<std::remove_reference_t<T>>; // A transform that flattens future expressions into a tuple. struct future_transform { // Transform a terminal into its contained tuple. template <typename T> auto operator() ( future_expr< boost::yap::expr_kind::terminal, boost::hana::tuple<T> > const & term ) { return term.elements; } // Transform left || right -> transform(left). template <typename T, typename U> auto operator() ( future_expr< boost::yap::expr_kind::logical_or, boost::hana::tuple<T, U> > const & or_expr ) { // Recursively transform the left side, and return the result. // Without the recursion, we might return a terminal expression here // insead of a tuple. return boost::yap::transform(boost::yap::left(or_expr), *this); } // Transform left && right -> concat(transform(left), transform(right)). template <typename T, typename U> auto operator() ( future_expr< boost::yap::expr_kind::logical_and, boost::hana::tuple<T, U> > const & and_expr ) { // Recursively transform each side, then combine the resulting tuples // into a single tuple result. return boost::hana::concat( boost::yap::transform(boost::yap::left(and_expr), *this), boost::yap::transform(boost::yap::right(and_expr), *this) ); } }; template <boost::yap::expr_kind Kind, typename Tuple> auto future_expr<Kind, Tuple>::get () const { return boost::yap::transform(*this, future_transform{}); } // TEST CASES struct A {}; struct B {}; struct C {}; // Called "vector" just so the code in main() will match the original Proto // example. template <typename ...T> using vector = boost::hana::tuple<T...>; int main() { future<A> a; future<B> b; future<C> c; future<vector<A,B> > ab; // Verify that various future groups have the // correct return types. A t0 = a.get(); vector<A, B, C> t1 = (a && b && c).get(); vector<A, C> t2 = ((a || a) && c).get(); vector<A, B, C> t3 = ((a && b || a && b) && c).get(); vector<vector<A, B>, C> t4 = ((ab || ab) && c).get(); return 0; }
Here we adapt an automatic differentiation library to use Boost.YAP for specifying the equations it operates on.
Autodiff is a pretty small library, and doesn't cover every possible input
expression. What it covers is simple arithmetic, and the well-known functions
sin, cos,
sqrt, and pow.
Here is how you would form an input to the library using its API. This is taken from the test program that comes with the library.
Node* build_linear_fun1_manually(vector<Node*>& list) { //f(x1,x2,x3) = -5*x1+sin(10)*x1+10*x2-x3/6 PNode* v5 = create_param_node(-5); PNode* v10 = create_param_node(10); PNode* v6 = create_param_node(6); VNode* x1 = create_var_node(); VNode* x2 = create_var_node(); VNode* x3 = create_var_node(); OPNode* op1 = create_binary_op_node(OP_TIMES,v5,x1); //op1 = v5*x1 OPNode* op2 = create_uary_op_node(OP_SIN,v10); //op2 = sin(v10) OPNode* op3 = create_binary_op_node(OP_TIMES,op2,x1); //op3 = op2*x1 OPNode* op4 = create_binary_op_node(OP_PLUS,op1,op3); //op4 = op1 + op3 OPNode* op5 = create_binary_op_node(OP_TIMES,v10,x2); //op5 = v10*x2 OPNode* op6 = create_binary_op_node(OP_PLUS,op4,op5); //op6 = op4+op5 OPNode* op7 = create_binary_op_node(OP_DIVID,x3,v6); //op7 = x3/v6 OPNode* op8 = create_binary_op_node(OP_MINUS,op6,op7); //op8 = op6 - op7 x1->val = -1.9; x2->val = 2; x3->val = 5./6.; list.push_back(x1); list.push_back(x2); list.push_back(x3); return op8; }
I have a lot of trouble understanding what's going on here, and even more verifying that the expression written in the comment is actually what the code produces. Let's see if we can do better.
First, we start with a custom expression template, autodiff_expr.
It supports simple arithmetic, but notice it has no call operator —
we don't want (a
+ b)() to be a valid expression.
template <boost::yap::expr_kind Kind, typename Tuple> struct autodiff_expr { static boost::yap::expr_kind const kind = Kind; Tuple elements; }; BOOST_YAP_USER_UNARY_OPERATOR(negate, autodiff_expr, autodiff_expr) BOOST_YAP_USER_BINARY_OPERATOR(plus, autodiff_expr, autodiff_expr) BOOST_YAP_USER_BINARY_OPERATOR(minus, autodiff_expr, autodiff_expr) BOOST_YAP_USER_BINARY_OPERATOR(multiplies, autodiff_expr, autodiff_expr) BOOST_YAP_USER_BINARY_OPERATOR(divides, autodiff_expr, autodiff_expr)
We're going to be using a lot of placeholders in our Autodiff expressions,
and it sure would be nice if they were autodiff_exprs
and not expression<>s, so that only our
desired operators are in play. To do this, we define an operator that produces
placeholder literals, using the BOOST_YAP_USER_LITERAL_PLACEHOLDER_OPERATOR
macro:
namespace autodiff_placeholders { // This defines a placeholder literal operator that creates autodiff_expr // placeholders. BOOST_YAP_USER_LITERAL_PLACEHOLDER_OPERATOR(autodiff_expr) }
Now, how about the functions we need to support, and where do we put the call operator? In other examples we created terminal subclasses or templates to get special behavior on terminals. In this case, we want to create a function-terminal template:
template <OPCODE Opcode> struct autodiff_fn_expr : autodiff_expr<boost::yap::expr_kind::terminal, boost::hana::tuple<OPCODE>> { autodiff_fn_expr () : autodiff_expr {boost::hana::tuple<OPCODE>{Opcode}} {} BOOST_YAP_USER_CALL_OPERATOR_N(::autodiff_expr, 1); }; // Someone included <math.h>, so we have to add trailing underscores. autodiff_fn_expr<OP_SIN> const sin_; autodiff_fn_expr<OP_COS> const cos_; autodiff_fn_expr<OP_SQRT> const sqrt_;
OPCODE is an enumeration
in Autodiff. We use it as a non-type template parameter for convenience
when declaring sin_ and
friends. All we really need is for the OPCODE
to be the value of the terminals we produce, and for these function-terminals
to have the call operator.
![[Note]](../../../doc/src/images/note.png) |
Note |
|---|---|
Using |
Now, some tranforms:
struct xform { // Create a var-node for each placeholder when we see it for the first // time. template <long long I> Node * operator() (boost::yap::expr_tag<boost::yap::expr_kind::terminal>, boost::yap::placeholder<I>) { if (list_.size() < I) list_.resize(I); auto & retval = list_[I - 1]; if (retval == nullptr) retval = create_var_node(); return retval; } // Create a param-node for every numeric terminal in the expression. Node * operator() (boost::yap::expr_tag<boost::yap::expr_kind::terminal>, double x) { return create_param_node(x); } // Create a "uary" node for each call expression, using its OPCODE. template <typename Expr> Node * operator() (boost::yap::expr_tag<boost::yap::expr_kind::call>, OPCODE opcode, Expr const & expr) { return create_uary_op_node( opcode, boost::yap::transform(boost::yap::as_expr<autodiff_expr>(expr), *this) ); } template <typename Expr> Node * operator() (boost::yap::expr_tag<boost::yap::expr_kind::negate>, Expr const & expr) { return create_uary_op_node( OP_NEG, boost::yap::transform(boost::yap::as_expr<autodiff_expr>(expr), *this) ); } // Define a mapping from binary arithmetic expr_kind to OPCODE... static OPCODE op_for_kind (boost::yap::expr_kind kind) { switch (kind) { case boost::yap::expr_kind::plus: return OP_PLUS; case boost::yap::expr_kind::minus: return OP_MINUS; case boost::yap::expr_kind::multiplies: return OP_TIMES; case boost::yap::expr_kind::divides: return OP_DIVID; default: assert(!"This should never execute"); return OPCODE{}; } assert(!"This should never execute"); return OPCODE{}; } // ... and use it to handle all the binary arithmetic operators. template <boost::yap::expr_kind Kind, typename Expr1, typename Expr2> Node * operator() (boost::yap::expr_tag<Kind>, Expr1 const & expr1, Expr2 const & expr2) { return create_binary_op_node( op_for_kind(Kind), boost::yap::transform(boost::yap::as_expr<autodiff_expr>(expr1), *this), boost::yap::transform(boost::yap::as_expr<autodiff_expr>(expr2), *this) ); } vector<Node *> & list_; };
We need a function to tie everything together, since the transforms cannot fill in the values for the placeholders.
template <typename Expr, typename ...T> Node * to_auto_diff_node (Expr const & expr, vector<Node *> & list, T ... args) { Node * retval = nullptr; // This fills in list as a side effect. retval = boost::yap::transform(expr, xform{list}); assert(list.size() == sizeof...(args)); // Fill in the values of the value-nodes in list with the "args" // parameter pack. auto it = list.begin(); boost::hana::for_each( boost::hana::make_tuple(args ...), [&it](auto x) { Node * n = *it; VNode * v = boost::polymorphic_downcast<VNode *>(n); v->val = x; ++it; } ); return retval; }
Finally, here is the Boost.YAP version of the function we started with:
Node* build_linear_fun1(vector<Node*>& list) { //f(x1,x2,x3) = -5*x1+sin(10)*x1+10*x2-x3/6 using namespace autodiff_placeholders; return to_auto_diff_node( -5 * 1_p + sin_(10) * 1_p + 10 * 2_p - 3_p / 6, list, -1.9, 2, 5./6. ); }
Sometimes it can be useful only to transform the terminals in an expression.
For instance, if you have some type you use for SIMD operations called
simd<double>,
you may want to replace all the double
terminals with simd<double>.
Perhaps you just want to change out double
for float, or int for std::size_t.
You get the idea.
In this example, we're replacing all the terminals with something essentially
arbitrary, the sequence of integer terminals N, N + 1,
N +
2, .... This makes it easier to observe the
result of the replacement in a simple example.
#include <boost/yap/yap.hpp> struct iota_terminal_transform { // Base case. Note that we're not treating placeholders specially for this // example (they're easy to special-case if necessary). template<typename T> auto operator()(boost::yap::expr_tag<boost::yap::expr_kind::terminal>, T && t) { // Like the std::iota() algorithm, we create replacement int terminals // with the values index_, index_ + 1, index_ + 2, etc. return boost::yap::make_terminal(index_++); } // Recursive case: Match any call expression. template<typename CallableExpr, typename... Arg> auto operator()(boost::yap::expr_tag<boost::yap::expr_kind::call>, CallableExpr callable, Arg &&... arg) { // Even though the callable in a call expression is technically a // terminal, it doesn't make a lot of sense to replace it with an int, // so we'll only transform the argument subexpressions. return boost::yap::make_expression<boost::yap::expr_kind::call>( boost::yap::as_expr(callable), boost::yap::transform(boost::yap::as_expr(arg), *this)...); } int index_; }; int sum(int a, int b) { return a + b; } int main() { { // This simple sum(8, 8) expression requires both overloads of // iota_terminal_transform. auto expr = boost::yap::make_terminal(sum)(8, 8); assert(evaluate(expr) == 16); auto iota_expr = boost::yap::transform(expr, iota_terminal_transform{1}); assert(evaluate(iota_expr) == 3); } { // This expression requires only the terminal case of // iota_terminal_transform. auto expr = -(boost::yap::make_terminal(8) + 8); assert(evaluate(expr) == -16); auto iota_expr = boost::yap::transform(expr, iota_terminal_transform{0}); assert(evaluate(iota_expr) == -1); } { // Like the first expression above, this expression requires both // overloads of iota_terminal_transform. auto expr = boost::yap::make_terminal(sum)(-(boost::yap::make_terminal(8) + 8), 0); assert(evaluate(expr) == -16); auto iota_expr = boost::yap::transform(expr, iota_terminal_transform{0}); assert(evaluate(iota_expr) == -3); } }
Let's revisit the pipable standard algorithm example from the intro. Here's how you might implement it.
#include <boost/yap/algorithm.hpp> #include <algorithm> #include <vector> // An enum to represent all the standard algorithms we want to adapt. In this // example, we only care about std::sort() and std::unique(). enum class algorithm_t { sort, unique }; // Just about the simplest range template you could construct. Nothing fancy. template<typename Iter> struct simple_range { Iter begin() const { return first_; } Iter end() const { return last_; } Iter first_; Iter last_; }; // This simply calls the standard algorithm that corresponds to "a". This // certainly won't work for all the algorithms, but it works for many of them // that just take a begin/end pair. template<typename Range> auto call_algorithm(algorithm_t a, Range & r) { simple_range<decltype(r.begin())> retval{r.begin(), r.end()}; if (a == algorithm_t::sort) { std::sort(r.begin(), r.end()); } else if (a == algorithm_t::unique) { retval.last_ = std::unique(r.begin(), r.end()); } return retval; } // This is the transform that evaluates our piped expressions. It returns a // simple_range<>, not a Yap expression. struct algorithm_eval { // A pipe should always have a Yap expression on the left and an // algorithm_t terminal on the right. template<typename LExpr> auto operator()( boost::yap::expr_tag<boost::yap::expr_kind::bitwise_or>, LExpr && left, algorithm_t right) { // Recursively evaluate the left ... auto const left_result = boost::yap::transform(std::forward<LExpr>(left), *this); // ... and use the result to call the function on the right. return call_algorithm(right, left_result); } // A call operation is evaluated directly. Note that the range parameter // is taken as an lvalue reference, to prevent binding to a temporary and // taking dangling references to its begin and end. We let the compiler // deduce whether the lvalue reference is const. template<typename Range> auto operator()( boost::yap::expr_tag<boost::yap::expr_kind::call>, algorithm_t a, Range & r) { return call_algorithm(a, r); } }; // This is the expression template we use for the general case of a pipable // algorithm expression. Terminals are handled separately. template<boost::yap::expr_kind Kind, typename Tuple> struct algorithm_expr { static boost::yap::expr_kind const kind = Kind; Tuple elements; // This is how we get the nice initializer semantics we see in the example // usage below. This is a bit limited though, because we always create a // temporary. It might therefore be better just to create algorithm_expr // expressions, call yap::evaluate(), and then use the sequence containers // assign() member function to do the actual assignment. template<typename Assignee> operator Assignee() const { // Exercise left for the reader: static_assert() that Assignee is some // sort of container type. auto const range = boost::yap::transform(*this, algorithm_eval{}); return Assignee(range.begin(), range.end()); } }; // This is a bit loose, because it allows us to write "sort(v) | unique(u)" or // similar. It works fine for this example, but in production code you may // want to write out the functions generated by this macro, and add SFINAE or // concepts constraints on the right template parameter. BOOST_YAP_USER_BINARY_OPERATOR(bitwise_or, algorithm_expr, algorithm_expr) // It's useful to specially handle terminals, because we want a different set // of operations to apply to them. We don't want "sort(x)(y)" to be // well-formed, for instance, or "sort | unique" either. struct algorithm { static boost::yap::expr_kind const kind = boost::yap::expr_kind::terminal; boost::hana::tuple<algorithm_t> elements; BOOST_YAP_USER_CALL_OPERATOR_N(::algorithm_expr, 1) }; // Here are ready-made Yap terminals, one for each algorithm enumerated in // algorithm_t. constexpr algorithm sort{{algorithm_t::sort}}; constexpr algorithm unique{{algorithm_t::unique}}; int main() { { std::vector<int> v1 = {0, 2, 2, 7, 1, 3, 8}; std::sort(v1.begin(), v1.end()); auto it = std::unique(v1.begin(), v1.end()); std::vector<int> const v2(v1.begin(), it); assert(v2 == std::vector<int>({0, 1, 2, 3, 7, 8})); } { std::vector<int> v1 = {0, 2, 2, 7, 1, 3, 8}; std::vector<int> const v2 = sort(v1) | unique; assert(v2 == std::vector<int>({0, 1, 2, 3, 7, 8})); } }
Boost.Phoenix has a thing called let().
It introduces named reusable values that are usable in subsequent expressions.
This example is something simliar, though not exactly like Phoenix's version.
In Phoenix, a let placeholder is only evaluated once, whereas the example
below does something more like macro substitution; each let-placeholder
is replaced with its initializing expression everywhere it is used.
This example uses C++17's if constexpr (),
simply because it makes the example shorter and easier to digest. The
if constexpr
() bits are not strictly necessary.
#include <boost/yap/yap.hpp> #include <boost/hana/map.hpp> #include <boost/hana/at_key.hpp> #include <boost/hana/contains.hpp> #include <boost/hana/keys.hpp> #include <vector> #include <iostream> // Here, we introduce special let-placeholders, so we can use them along side // the normal YAP placeholders without getting them confused. template<long long I> struct let_placeholder : boost::hana::llong<I> { }; // Replaces each let-terminal with the expression with which it was // initialized in let(). So in 'let(_a = foo)[ _a + 1 ]', this transform will // be used on '_a + 1' to replace '_a' with 'foo'. The map_ member holds the // mapping of let-placeholders to their initializers. template<typename ExprMap> struct let_terminal_transform { // This matches only let-placeholders. For each one matched, we look up // its initializer in map_ and return it. template<long long I> auto operator()( boost::yap::expr_tag<boost::yap::expr_kind::terminal>, let_placeholder<I> i) { // If we have an entry in map_ for this placeholder, return the value // of the entry. Otherwise, pass i through as a terminal. if constexpr (boost::hana::contains( decltype(boost::hana::keys(map_))(), boost::hana::llong_c<I>)) { return map_[boost::hana::llong_c<I>]; } else { return boost::yap::make_terminal(i); } } ExprMap map_; }; // As you can see below, let() is an eager function; this template is used for // its return values. It contains the mapping from let-placeholders to // initializer expressions used to transform the expression inside '[]' after // a let()'. It also has an operator[]() member function that takes the // expression inside '[]' and returns a version of it with the // let-placeholders replaced. template<typename ExprMap> struct let_result { template<typename Expr> auto operator[](Expr && expr) { return boost::yap::transform( std::forward<Expr>(expr), let_terminal_transform<ExprMap>{map_}); } ExprMap map_; }; // Processes the expressions passed to let() one at a time, adding each one to // a Hana map of hana::llong<>s to YAP expressions. template<typename Map, typename Expr, typename... Exprs> auto let_impl(Map && map, Expr && expr, Exprs &&... exprs) { static_assert( Expr::kind == boost::yap::expr_kind::assign, "Expressions passed to let() must be of the form placeholder = Expression"); if constexpr (sizeof...(Exprs) == 0) { using I = typename std::remove_reference<decltype( boost::yap::value(boost::yap::left(expr)))>::type; auto const i = boost::hana::llong_c<I::value>; using map_t = decltype(boost::hana::insert( map, boost::hana::make_pair(i, boost::yap::right(expr)))); return let_result<map_t>{boost::hana::insert( map, boost::hana::make_pair(i, boost::yap::right(expr)))}; } else { using I = typename std::remove_reference<decltype( boost::yap::value(boost::yap::left(expr)))>::type; auto const i = boost::hana::llong_c<I::value>; return let_impl( boost::hana::insert( map, boost::hana::make_pair(i, boost::yap::right(expr))), std::forward<Exprs>(exprs)...); } } // Takes N > 0 expressions of the form 'placeholder = expr', and returns an // object with an overloaded operator[](). template<typename Expr, typename... Exprs> auto let(Expr && expr, Exprs &&... exprs) { return let_impl( boost::hana::make_map(), std::forward<Expr>(expr), std::forward<Exprs>(exprs)...); } int main() { // Some handy terminals -- the _a and _b let-placeholders and std::cout as // a YAP terminal. boost::yap::expression< boost::yap::expr_kind::terminal, boost::hana::tuple<let_placeholder<0>>> const _a; boost::yap::expression< boost::yap::expr_kind::terminal, boost::hana::tuple<let_placeholder<1>>> const _b; auto const cout = boost::yap::make_terminal(std::cout); using namespace boost::yap::literals; { auto expr = let(_a = 2)[_a + 1]; assert(boost::yap::evaluate(expr) == 3); } { auto expr = let(_a = 123, _b = 456)[_a + _b]; assert(boost::yap::evaluate(expr) == 123 + 456); } // This prints out "0 0", because 'i' is passed as an lvalue, so its // decrement is visible outside the let expression. { int i = 1; boost::yap::evaluate(let(_a = 1_p)[cout << --_a << ' '], i); std::cout << i << std::endl; } // Prints "Hello, World" due to let()'s scoping rules. { boost::yap::evaluate( let(_a = 1_p, _b = 2_p) [ // _a here is an int: 1 let(_a = 3_p) // hides the outer _a [ cout << _a << _b // prints "Hello, World" ] ], 1, " World", "Hello," ); } std::cout << "\n"; // Due to the macro-substitution style that this example uses, this prints // "3132". Phoenix's let() prints "312", because it only evaluates '1_p // << 3' once. { boost::yap::evaluate( let(_a = 1_p << 3) [ _a << "1", _a << "2" ], std::cout ); } std::cout << "\n"; }
The main header you will always need to use Boost.YAP is the <boost/yap/algorithm.hpp>
header. If you want to ensure that you don't accidentally use expression<> (which I recommend),
just include this header and nothing else.
If you want to use the expression<>
reference expression template (great for prototyping, but not recommended
for production work), include the <boost/yap/expression.hpp>
header.
If you want to include all of the above, use the <boost/yap/yap.hpp>
header.
If you want to use print(), include the <boost/yap/print.hpp>
header; this header is not included in the <boost/yap/yap.hpp>
header.
BOOST_NO_CONSTEXPR_IF
is a macro that indicates whether the compiler has support for constexpr
if. It defaults to no. Define it to be a nonzero value if your compiler has
constexpr if support. Note that this is a temporary hack; this should eventually
be a Boost-wide macro.
Let's look at some assembly. All assembly here was produced with Clang 4.0
with -O3.
Given these definitions:
namespace user { struct number { double value; friend number operator+(number lhs, number rhs) { return number{lhs.value + rhs.value}; } friend number operator*(number lhs, number rhs) { return number{lhs.value * rhs.value}; } }; }
Here is a Boost.YAP-based arithmetic function:
user::number eval_as_yap_expr(user::number a_, user::number x_, user::number y_) { term<user::number> a{{a_}}; term<user::number> x{{x_}}; term<user::number> y{{y_}}; auto expr = (a * x + y) * (a * x + y) + (a * x + y); return yap::evaluate(expr); }
and the assembly it produces:
arithmetic_perf[0x100001c00] <+0>: pushq %rbp arithmetic_perf[0x100001c01] <+1>: movq %rsp, %rbp arithmetic_perf[0x100001c04] <+4>: mulsd %xmm1, %xmm0 arithmetic_perf[0x100001c08] <+8>: addsd %xmm2, %xmm0 arithmetic_perf[0x100001c0c] <+12>: movapd %xmm0, %xmm1 arithmetic_perf[0x100001c10] <+16>: mulsd %xmm1, %xmm1 arithmetic_perf[0x100001c14] <+20>: addsd %xmm0, %xmm1 arithmetic_perf[0x100001c18] <+24>: movapd %xmm1, %xmm0 arithmetic_perf[0x100001c1c] <+28>: popq %rbp arithmetic_perf[0x100001c1d] <+29>: retq
And for the equivalent function using builtin expressions:
user::number eval_as_cpp_expr(user::number a, user::number x, user::number y) { return (a * x + y) * (a * x + y) + (a * x + y); }
the assembly is:
arithmetic_perf[0x100001e10] <+0>: pushq %rbp arithmetic_perf[0x100001e11] <+1>: movq %rsp, %rbp arithmetic_perf[0x100001e14] <+4>: mulsd %xmm1, %xmm0 arithmetic_perf[0x100001e18] <+8>: addsd %xmm2, %xmm0 arithmetic_perf[0x100001e1c] <+12>: movapd %xmm0, %xmm1 arithmetic_perf[0x100001e20] <+16>: mulsd %xmm1, %xmm1 arithmetic_perf[0x100001e24] <+20>: addsd %xmm0, %xmm1 arithmetic_perf[0x100001e28] <+24>: movapd %xmm1, %xmm0 arithmetic_perf[0x100001e2c] <+28>: popq %rbp arithmetic_perf[0x100001e2d] <+29>: retq
If we increase the number of terminals by a factor of four:
user::number eval_as_yap_expr_4x(user::number a_, user::number x_, user::number y_) { term<user::number> a{{a_}}; term<user::number> x{{x_}}; term<user::number> y{{y_}}; auto expr = (a * x + y) * (a * x + y) + (a * x + y) + (a * x + y) * (a * x + y) + (a * x + y) + (a * x + y) * (a * x + y) + (a * x + y) + (a * x + y) * (a * x + y) + (a * x + y); return yap::evaluate(expr); }
the results are the same: in this simple case, the Boost.YAP and builtin expressions result in the same object code.
However, increasing the number of terminals by an additional factor of 2.5 (for a total of 90 terminals), the inliner can no longer do as well for Boost.YAP expressions as for builtin ones.
More complex nonarithmetic code produces more mixed results. For example, here is a function using code from the Map Assign example:
std::map<std::string, int> make_map_with_boost_yap () { return map_list_of ("<", 1) ("<=",2) (">", 3) (">=",4) ("=", 5) ("<>",6) ; }
By contrast, here is the Boost.Assign version of the same function:
std::map<std::string, int> make_map_with_boost_assign () { return boost::assign::map_list_of ("<", 1) ("<=",2) (">", 3) (">=",4) ("=", 5) ("<>",6) ; }
Here is how you might do it "manually":
std::map<std::string, int> make_map_manually () { std::map<std::string, int> retval; retval.emplace("<", 1); retval.emplace("<=",2); retval.emplace(">", 3); retval.emplace(">=",4); retval.emplace("=", 5); retval.emplace("<>",6); return retval; }
Finally, here is the same map created from an initializer list:
std::map<std::string, int> make_map_inializer_list () { std::map<std::string, int> retval = { {"<", 1}, {"<=",2}, {">", 3}, {">=",4}, {"=", 5}, {"<>",6} }; return retval; }
All of these produce roughly the same amount of assembly instructions. Benchmarking these four functions with Google Benchmark yields these results:
Table 48.5. Runtimes of Different Map Constructions
|
Function |
Time (ns) |
|---|---|
|
make_map_with_boost_yap() |
1285 |
|
make_map_with_boost_assign() |
1459 |
|
make_map_manually() |
985 |
|
make_map_inializer_list() |
954 |
The Boost.YAP-based implementation finishes in the middle of the pack.
In general, the expression trees produced by Boost.YAP get evaluated down to something close to the hand-written equivalent. There is an abstraction penalty, but it is small for reasonably-sized expressions.