Boost Graph Library: Maximum Cardinality Matching
template <typename Graph, typename MateMap>
void edmonds_maximum_cardinality_matching(const Graph& g, MateMap mate);
template <typename Graph, typename MateMap, typename VertexIndexMap>
void edmonds_maximum_cardinality_matching(const Graph& g, MateMap mate, VertexIndexMap vm);
template <typename Graph, typename MateMap>
bool checked_edmonds_maximum_cardinality_matching(const Graph& g, MateMap mate);
template <typename Graph, typename MateMap, typename VertexIndexMap>
bool checked_edmonds_maximum_cardinality_matching(const Graph& g, MateMap mate, VertexIndexMap vm);
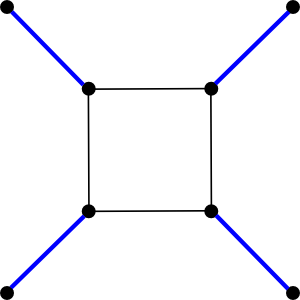
A matching is a subset of the edges
of a graph such that no two edges share a common vertex.
Two different matchings in the same graph are illustrated below (edges in the
matching are colored blue.) The matching on the left is a maximal matching,
meaning that its size can't be increased by adding edges. The matching on the
right is a maximum cardinality matching, meaning that is has maximum size
over all matchings in the graph.
Both edmonds_maximum_cardinality_matching and
checked_edmonds_maximum_cardinality_matching find the
maximum cardinality matching in any undirected graph. The matching is returned in a
MateMap, which is a
ReadWritePropertyMap
that maps vertices to vertices. In the mapping returned, each vertex is either mapped
to the vertex it's matched to, or to graph_traits<Graph>::null_vertex() if it
doesn't participate in the matching. If no VertexIndexMap is provided, both functions
assume that the VertexIndexMap is provided as an internal graph property accessible
by calling get(vertex_index,g). The only difference between
edmonds_maximum_cardinality_matching and
checked_edmonds_maximum_cardinality_matching is that as a final step,
the latter algorithm runs a simple verification on the matching computed and
returns true if and only if the matching is indeed
a maximum cardinality matching.
Given a matching M, any vertex that isn't covered by an edge in M is called free. Any
simple path containing exactly 2n + 1 edges that starts and ends at free vertices and contains
n edges from M is called an alternating path. Given an alternating path p, all matching and
non-matching edges on p can be swapped, resulting in a new matching that's larger than the
original matching by exactly one edge. This method of incrementally increasing the size of matching, along
with the following fact, forms the basis of Edmonds' matching algorithm:
An alternating path through the matching M exists if and only if M is not a maximum cardinality matching.
The difficult part is, of course, finding an augmenting path whenever one exists.
The algorithm we use for finding a maximum cardinality matching consists of three basic steps:
- Create an initial matching.
- Repeatedly find an augmenting path and use it to increase the size of the matching until no augmenting path exists.
- Verify that the matching found is a maximum cardinality matching.
If you use
checked_edmonds_maximum_cardinality_matching or
edmonds_maximum_cardinality_matching, all three of these
steps are chosen for you, but it's easy to plug in different algorithms for these three steps
using a generic matching function discussed below - in fact, both
checked_edmonds_maximum_cardinality_matching
and
edmonds_maximum_cardinality_matching are just inlined specializations of this function.
When quoting time bounds for algorithms, we assume that VertexIndexMap is a property map
that allows for constant-time mapping between vertices and indices (which is easily achieved if,
for instance, the vertices are stored in contiguous memory.) We use n and m to represent the size
of the vertex and edge sets, respectively, of the input graph.
Algorithms for Creating an Initial Matching
- empty_matching: Takes time O(n) to initialize the empty matching.
- greedy_matching: The matching obtained by iterating through the edges and adding an edge
if it doesn't conflict with the edges already in the matching. This matching is maximal, and is therefore
guaranteed to contain at least half of the edges that a maximum matching has. Takes time O(m log n).
- extra_greedy_matching: Sorts the edges in increasing order of the degree of the vertices
contained in each edge, then constructs a greedy matching from those edges. Also a maximal matching, and can
sometimes be much closer to the maximum cardinality matching than a simple greedy_matching.
Takes time O(m log n), but the constants involved make this a slower algorithm than
greedy_matching.
Algorithms for Finding an Augmenting Path
- edmonds_augmenting_path_finder: Finds an augmenting path in time O(m alpha(m,n)),
where alpha(m,n) is an inverse of the Ackerman function. alpha(m,n) is one of the slowest
growing functions that occurs naturally in computer science; essentially, alpha(m,n) ≤ 4 for any
graph that we'd ever hope to run this algorithm on. Since we arrive at a maximum cardinality matching after
augmenting O(n) matchings, the entire algorithm takes time O(mn alpha(m,n)). Edmonds' original
algorithm appeared in [64], but our implementation of
Edmonds' algorithm closely follows Tarjan's
description of the algorithm from [27].
- no_augmenting_path_finder: Can be used if no augmentation of the initial matching is desired.
Verification Algorithms
- maximum_cardinality_matching_verifier: Returns true if and only if the matching found is a
maximum cardinality matching. Takes time O(m alpha(m,n)), which is on the order of a single iteration
of Edmonds' algorithm.
- no_matching_verifier: Always returns true
Why is a verification algorithm needed? Edmonds' algorithm is fairly complex, and it's nearly
impossible for a human without a few days of spare time to figure out if the matching produced by
edmonds_matching on a graph with, say, 100 vertices and 500 edges is indeed a maximum cardinality
matching. A verification algorithm can do this mechanically, and it's much easier to verify by inspection
that the verification algorithm has been implemented correctly than it is to verify by inspection that
Edmonds' algorithm has been implemented correctly.
The Boost Graph library makes it incredibly simple to perform the subroutines needed by the verifier
(such as finding all the connected components of odd cardinality in a graph, or creating the induced graph
on all vertices with a certain label) in just a few lines of code.
Understanding how the verifier works requires a few graph-theoretic facts.
Let m(G) be the size of a maximum cardinality matching in the graph G.
Denote by o(G) the number of connected components in G of odd cardinality, and for a set of
vertices X, denote by G - X the induced graph on the vertex set V(G) - X. Then the
Tutte-Berge Formula says that
2 * m(G) = min ( |V(G)| + |X| - o(G-X) )
Where the minimum is taken over all subsets
X of the vertex set
V(G). A side effect of the
Edmonds Blossom-Shrinking algorithm is that it computes what is known as the Edmonds-Gallai decomposition
of a graph: it decomposes the graph into three disjoint sets of vertices, one of which achieves the minimum
in the Tutte-Berge Formula.
An outline of our verification procedure is:
Given a
Graph g and
MateMap mate,
- Check to make sure that mate is a valid matching on g.
- Run edmonds_augmenting_path_finder once on g and mate. If it finds an augmenting
path, the matching isn't a maximum cardinality matching. Otherwise, we retrieve a copy of the vertex_state
map used by the edmonds_augmenting_path_finder. The Edmonds-Gallai decomposition tells us that the set
of vertices labeled V_ODD by the vertex_state map can be used as the set X to achieve the
minimum in the Tutte-Berge Formula.
- Count the number of vertices labeled V_ODD, store this in num_odd_vertices.
- Create a filtered_graph
consisting of all vertices that aren't labeled V_ODD. Count the number of odd connected components
in this graph and store the result in num_odd_connected_components.
- Test to see if equality holds in the Tutte-Berge formula using |X| = num_odd_vertices and o(G-X) = num_odd_connected_components. Return true if it holds, false otherwise.
Assuming these steps are implemented correctly, the verifier will never return a false positive,
and will only return a false negative if
edmonds_augmenting_path_finder doesn't compute the
vertex_state map correctly, in which case the
edmonds_augmenting_path_finder
isn't working correctly.
Creating Your Own Matching Algorithms
Creating a matching algorithm is as simple as plugging the algorithms described above into a generic
matching function, which has the following signature:
template <typename Graph,
typename MateMap,
typename VertexIndexMap,
template <typename, typename, typename> class AugmentingPathFinder,
template <typename, typename> class InitialMatchingFinder,
template <typename, typename, typename> class MatchingVerifier>
bool matching(const Graph& g, MateMap mate, VertexIndexMap vm)
The matching functions provided for you are just inlined specializations of this function:
edmonds_maximum_cardinality_matching uses
edmonds_augmenting_path_finder
as the
AugmentingPathFinder,
extra_greedy_matching as the
InitialMatchingFinder,
and
no_matching_verifier as the
MatchingVerifier.
checked_edmonds_maximum_cardinality_matching uses the same parameters except that
maximum_cardinality_matching_verifier is used for the
MatchingVerifier.
These aren't necessarily the best choices for any situation - for example, it's been claimed in the literature
that for sparse graphs, Edmonds' algorithm converges to the maximum cardinality matching more quickly if it
isn't supplied with an intitial matching. Such an algorithm can be easily assembled by calling matching with
- AugmentingPathFinder = edmonds_augmenting_path_finder
- InitialMatchingFinder = empty_matching
and choosing the
MatchingVerifier depending on how careful you're feeling.
Suppose instead that you want a relatively large matching quickly, but are not exactly interested in a maximum matching.
Both extra_greedy_matching and greedy_matching find maximal matchings, which means they're guaranteed to be at
least half the size of a maximum cardinality matching, so you could call matching with
- AugmentingPathFinder = no_augmenting_path_finder
- InitialMatchingFinder = extra_greedy_matching
- MatchingVerifier = maximum_cardinality_matching_verifier
The resulting algorithm will find an extra greedy matching in time
O(m log n) without looking for
augmenting paths. As a bonus, the return value of this function is true if and only if the extra greedy
matching happens to be a maximum cardinality matching.
Where Defined
boost/graph/max_cardinality_matching.hpp
Parameters
IN:
const Graph& g
An undirected graph. The graph type must be a model of
Vertex and Edge List Graph and
Incidence Graph.
IN:
VertexIndexMap vm
Must be a model of ReadablePropertyMap, mapping vertices to integer indices.
OUT:
MateMap mate
Must be a model of ReadWritePropertyMap, mapping
vertices to vertices. For any vertex v in the graph, get(mate,v) will be the vertex that v is matched to, or
graph_traits::null_vertex() if v isn't matched.
Complexity
Let m and n be the number of edges and vertices in the input graph, respectively. Assuming the
VertexIndexMap supplied allows constant-time lookups, the time complexity for both
edmonds_matching and checked_edmonds_matching is O(mn alpha(m,n)).
alpha(m,n) is a slow growing function that is at most 4 for any feasible input.
Example
The file example/matching_example.cpp
contains an example.
 Boost
C++ Libraries
Boost
C++ Libraries