 Boost
C++ Libraries
Boost
C++ Libraries
...one of the most highly
regarded and expertly designed C++ library projects in the
world.
— Herb Sutter and Andrei
Alexandrescu, C++
Coding Standards
 Boost
C++ Libraries
Boost
C++ Libraries
...one of the most highly
regarded and expertly designed C++ library projects in the
world.
— Herb Sutter and Andrei
Alexandrescu, C++
Coding Standards
Once you have calculated the standard deviation for your data, a legitimate question to ask is "How reliable is the calculated standard deviation?". For this situation the Chi Squared distribution can be used to calculate confidence intervals for the standard deviation.
The full example code & sample output is in chi_square_std_deviation_test.cpp.
We'll begin by defining the procedure that will calculate and print out the confidence intervals:
void confidence_limits_on_std_deviation( double Sd, // Sample Standard Deviation unsigned N) // Sample size {
We'll begin by printing out some general information:
cout << "________________________________________________\n" "2-Sided Confidence Limits For Standard Deviation\n" "________________________________________________\n\n"; cout << setprecision(7); cout << setw(40) << left << "Number of Observations" << "= " << N << "\n"; cout << setw(40) << left << "Standard Deviation" << "= " << Sd << "\n";
and then define a table of significance levels for which we'll calculate intervals:
double alpha[] = { 0.5, 0.25, 0.1, 0.05, 0.01, 0.001, 0.0001, 0.00001 };
The distribution we'll need to calculate the confidence intervals is a Chi Squared distribution, with N-1 degrees of freedom:
chi_squared dist(N - 1);
For each value of alpha, the formula for the confidence interval is given by:

Where 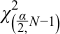 is the upper critical value, and
is the upper critical value, and  is
the lower critical value of the Chi Squared distribution.
is
the lower critical value of the Chi Squared distribution.
In code we begin by printing out a table header:
cout << "\n\n" "_____________________________________________\n" "Confidence Lower Upper\n" " Value (%) Limit Limit\n" "_____________________________________________\n";
and then loop over the values of alpha and calculate the intervals for each: remember that the lower critical value is the same as the quantile, and the upper critical value is the same as the quantile from the complement of the probability:
for(unsigned i = 0; i < sizeof(alpha)/sizeof(alpha[0]); ++i) { // Confidence value: cout << fixed << setprecision(3) << setw(10) << right << 100 * (1-alpha[i]); // Calculate limits: double lower_limit = sqrt((N - 1) * Sd * Sd / quantile(complement(dist, alpha[i] / 2))); double upper_limit = sqrt((N - 1) * Sd * Sd / quantile(dist, alpha[i] / 2)); // Print Limits: cout << fixed << setprecision(5) << setw(15) << right << lower_limit; cout << fixed << setprecision(5) << setw(15) << right << upper_limit << endl; } cout << endl;
To see some example output we'll use the gear data from the NIST/SEMATECH e-Handbook of Statistical Methods.. The data represents measurements of gear diameter from a manufacturing process.
________________________________________________
2-Sided Confidence Limits For Standard Deviation
________________________________________________
Number of Observations = 100
Standard Deviation = 0.006278908
_____________________________________________
Confidence Lower Upper
Value (%) Limit Limit
_____________________________________________
50.000 0.00601 0.00662
75.000 0.00582 0.00685
90.000 0.00563 0.00712
95.000 0.00551 0.00729
99.000 0.00530 0.00766
99.900 0.00507 0.00812
99.990 0.00489 0.00855
99.999 0.00474 0.00895
So at the 95% confidence level we conclude that the standard deviation is between 0.00551 and 0.00729.
Similarly, we can also list the confidence intervals for the standard deviation for the common confidence levels 95%, for increasing numbers of observations.
The standard deviation used to compute these values is unity, so the limits listed are multipliers for any particular standard deviation. For example, given a standard deviation of 0.0062789 as in the example above; for 100 observations the multiplier is 0.8780 giving the lower confidence limit of 0.8780 * 0.006728 = 0.00551.
____________________________________________________
Confidence level (two-sided) = 0.0500000
Standard Deviation = 1.0000000
________________________________________
Observations Lower Upper
Limit Limit
________________________________________
2 0.4461 31.9102
3 0.5207 6.2847
4 0.5665 3.7285
5 0.5991 2.8736
6 0.6242 2.4526
7 0.6444 2.2021
8 0.6612 2.0353
9 0.6755 1.9158
10 0.6878 1.8256
15 0.7321 1.5771
20 0.7605 1.4606
30 0.7964 1.3443
40 0.8192 1.2840
50 0.8353 1.2461
60 0.8476 1.2197
100 0.8780 1.1617
120 0.8875 1.1454
1000 0.9580 1.0459
10000 0.9863 1.0141
50000 0.9938 1.0062
100000 0.9956 1.0044
1000000 0.9986 1.0014
With just 2 observations the limits are from 0.445 up to to 31.9, so the standard deviation might be about half the observed value up to 30 times the observed value!
Estimating a standard deviation with just a handful of values leaves a very great uncertainty, especially the upper limit. Note especially how far the upper limit is skewed from the most likely standard deviation.
Even for 10 observations, normally considered a reasonable number, the range is still from 0.69 to 1.8, about a range of 0.7 to 2, and is still highly skewed with an upper limit twice the median.
When we have 1000 observations, the estimate of the standard deviation is starting to look convincing, with a range from 0.95 to 1.05 - now near symmetrical, but still about + or - 5%.
Only when we have 10000 or more repeated observations can we start to be reasonably confident (provided we are sure that other factors like drift are not creeping in).
For 10000 observations, the interval is 0.99 to 1.1 - finally a really convincing + or -1% confidence.