Polygon Sponsor
|
Voronoi Benchmark
There are not many known Voronoi libraries that are capable to satisfy
the
following set of conditions:
- could handle input data sets of points and segments
- give exact warranties about the algorithm robustness and
output topology
- compute coordinates of the output geometries within the
fixed relative precision
Below is the list of libraries included in this benchmark sorted by the
number of conditions each of them satisfies:
- Boost.Polygon Voronoi - satisfies all the conditions above,
implements sweep-line algorithm.
- CGAL - satisfies the first two conditions, implements
incremental algorithm. CGAL is a well-known
library in the computational geometry area, especially for its
robustness.
- S-Hull
- doesn't satisfy any of the above conditions. S-Hull is a non-robust
implementation of the sweep-hull algorithm used to construct Delaunay
triangulation of a set of points.
At the moment this benchmark includes only two robust implementations:
Boost.Polygon Voronoi and CGAL. Thus we are considering comparison of
those two to be of the most interest.
Other libraries (OpenVoronoi,
Triangle)
would be added to this benchmark
incrementally (we are open for suggestions).
Important
While results of this benchmark show complete dominance of
the Boost.Polygon Voronoi over the CGAL Delaunay Graph implementation,
we would like to make it clear
that both libraries use different approach to construct Voronoi
diagram. Thus there are problems where the CGAL's incremental approach
would
be still more vital than the sweep-line algorithm (e.g. input sites are
inserted as a live stream
data).
Voronoi Benchmark Details
The benchmark consists of the two parts:
Below we list important benchmark details that should be considered
while reviewing its results:
- We ensure that input data sets are the same for all
libraries by initializing random generator with the same seed
- We ensure that input data sets that consist of segments
don't contain intersections using Boost.Polygon functionality
- S-Hull's implementation doesn't process duplicate points
properly, thus those are eliminated before the algorithm execution
explicitly (Boost.Polygon Voronoi and CGAL do that implicitly)
- There is no Voronoi diagram data structure in CGAL/S-Hull.
That's why we use the segment Delaunay graph which is topologically
dual to the Voronoi diagram
- CGAL's and S-Hull's output Delaunay triangulation doesn't
contain information
about coordinates of the Voronoi vertices. We didn't include time to
compute Voronoi vertices and memory
storage required for those in this benchmark.
- Both Boost.Polygon Voronoi and CGAL process each input
segment
as 3 input objects (segment itself and its endpoints), thus the running
time and memory usage for Voronoi of segments would be at
least 3 times
slower than for Voronoi of points
The benchmark was executed on the following two system configurations:
Hardware: Intel i5-7600 2.8 GHz, 4GiB RAM.
OS: Windows 7 Professional 32-bit.
Libraries: Boost 1.48.0, CGAL-4.0.
Hardware: Intel i5-7600 2.8 GHz, 4GiB RAM.
OS: Ubuntu 11.10 64-bit.
Libraries: Boost 1.48.0, CGAL-4.0, GMP 5.0.4, MPFR 3.1.0 + cumulative
patch.
Voronoi Benchmark Results
Random Points Benchmark
Test specification
|
Average construction
time (in secs)
|
Number
of Points
|
Number
of Runs
|
Boost
Win-32
|
CGAL
Win-32
|
S-Hull
Win-32
|
Boost
Linux-64
|
CGAL
Linux-64
|
S-Hull
Linux-64
|
10
|
100000
|
0.000027
|
0.000116
|
0.000043
|
0.000013
|
0.000052
|
0.000012
|
100
|
10000
|
0.000392
|
0.002649
|
0.000521
|
0.000192
|
 0.001150
|
0.000139
|
1000
|
1000
|
0.004541
|
0.039140
|
0.007125
|
0.002130
|
0.016680
|
0.002010
|
10000
|
100
|
0.047540
|
0.684090
|
0.091640
|
0.022900
|
0.297900
|
0.028300
|
100000
|
10
|
0.530200
|
 16.904600
|
1.218000
|
0.274000
|
8.047000
|
0.432000
|
1000000
|
1
|
5.882000
|
566.056000
|
15.394000
|
3.290000
|
315.740000
|
6.350000
|
Random Segments Benchmark
Test specification
|
Average construction
time (in secs) |
Number
of Segments
|
Number
of Runs
|
Boost
Win-32
|
CGAL
Win-32
|
Boost
Linux-64
|
CGAL
Linux-64
|
10
|
100000
|
0.000290
|
0.001047
|
0.000165
|
0.000483
|
100
|
10000
|
0.003655
|
0.014812
|
0.002006
|
0.007006
|
1000
|
1000
|
0.038158
|
0.177315
|
0.020440
|
0.084000
|
10000
|
100
|
0.389470
|
2.561340
|
 0.209700
|
1.191900
|
100000
|
10
|
4.031300
|
49.314600
|
2.228000
|
23.538000
|
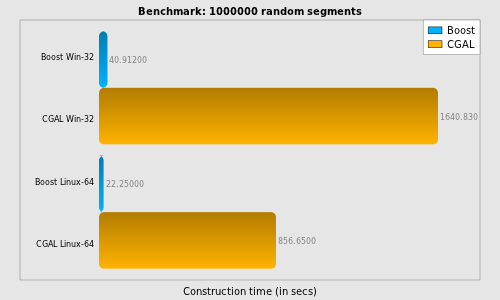
1000000
|
1
|
40.912000
|
1640.830000
|
22.250000
|
856.650000
|
Voronoi Benchmark Summary
The main conclusions for the benchmark results above are following:
- There is no input size range were CGAL would outperform
Boost.Polygon Voronoi. Even considering the fact that we didn't include
time it would take CGAL to compute coordinates of the Voronoi vertices.
- The more interesting fact is that robust implementation of
the Boost.Polygon Voronoi is faster than non-robust of
S-Hull (except small input sets of around 100 points on Linux-64).
- Logarithmic execution time shows that Boost.Polygon Voronoi
and S-Hull
have clear N*log(N) complexity, while this doesn't seem to be true for
CGAL (at least for large input data sets).
- Boost.Polygon Voronoi computes coordinates of the output
Voronoi vertices within 64 machine epsilon precision. There are no such
warranties for the CGAL library.
- Boost.Polygon Voronoi of points is 4 times faster for small
input data sets (10 points) and this factor grows up to 100 for large
input data sets (1000000 points).
- Boost.Polygon Voronoi of segments is 3 times faster for
small input data sets (10 segments) and this factor grows up to 40 for
large input data sets (1000000 segments).
- Boost.Polygon
Voronoi is capable to construct Voronoi of 10000 points or 1000
segments in 0.02 seconds. This allows to produce real time frame rate
for those quantities.
|
 Boost
C++ Libraries
Boost
C++ Libraries