 Boost
C++ Libraries
Boost
C++ Libraries
...one of the most highly
regarded and expertly designed C++ library projects in the
world.
— Herb Sutter and Andrei
Alexandrescu, C++
Coding Standards
 Boost
C++ Libraries
Boost
C++ Libraries
...one of the most highly
regarded and expertly designed C++ library projects in the
world.
— Herb Sutter and Andrei
Alexandrescu, C++
Coding Standards
Table of Contents
The Boost.Sort library provides a generic implementation of high-speed sorting algorithms that outperform those in the C++ standard in both average and worst case performance when there are over 1000 elements in the list to sort.
They fall back to STL std::sort on small data sets.
![[Warning]](../../../../doc/src/images/warning.png) |
Warning |
|---|---|
These algorithms all only work on random access iterators. |
They are hybrids using both radix and comparison-based sorting, specialized to sorting common data types, such as integers, floats, and strings.
These algorithms are encoded in a generic fashion and accept functors, enabling
them to sort any object that can be processed like these basic data types.
In the case of string_sort
Unlike many radix-based algorithms, the underlying spreadsortspreadsortstring_sort
Situations where spreadsort
spreadsort
Situations where spreadsort
spreadsortspreadsort
These functions are defined in namespace
boost::sort::spreadsort.
![[Tip]](../../../../doc/src/images/tip.png) |
Tip |
|---|---|
In the Boost.Sort C++ Reference section, click on the appropriate overload,
for example |
Each of integer_sortfloat_sortstring_sort
integer_sort(array.begin(), array.end()); float_sort(array.begin(), array.end()); string_sort(array.begin(), array.end());
The version with an overridden shift functor, providing flexibility in case
the operator>>
already does something other than a bitshift. The rightshift functor takes
two args, first the data type, and second a natural number of bits to shift
right.
For string_sortoperator[], taking a number
corresponding to the character offset, along with a second getlength functor to get the length of
the string in characters. In all cases, this operator must return an integer
type that compares with the operator< to provide the intended order (integers
can be negated to reverse their order).
In other words (aside from negative floats, which are inverted as ints):
rightshift(A, n) < rightshift(B, n) -> A < B A < B -> rightshift(A, 0) < rightshift(B, 0)
integer_sort(array.begin(), array.end(), rightshift());
string_sort(array.begin(), array.end(), bracket(), getsize());
See rightshiftsample.cpp for a working example of integer sorting with a rightshift functor.
And a version with a comparison functor for maximum flexibility. This functor must provide the same sorting order as the integers returned by the rightshift (aside from negative floats):
rightshift(A, n) < rightshift(B, n) -> compare(A, B) compare(A, B) -> rightshift(A, 0) < rightshift(B, 0)
integer_sort(array.begin(), array.end(), negrightshift(), std::greater<DATA_TYPE>());
Examples of functors are:
struct lessthan { inline bool operator()(const DATA_TYPE &x, const DATA_TYPE &y) const { return x.a < y.a; } };
struct bracket { inline unsigned char operator()(const DATA_TYPE &x, size_t offset) const { return x.a[offset]; } };
struct getsize { inline size_t operator()(const DATA_TYPE &x) const{ return x.a.size(); } };
and these functors are used thus:
string_sort(array.begin(), array.end(), bracket(), getsize(), lessthan());
See stringfunctorsample.cpp for a working example of sorting strings with all functors.
The spreadsort
The Spreadsort algorithm dynamically chooses either comparison-based or radix-based sorting when recursing, whichever provides better worst-case performance. This way worst-case performance is guaranteed to be the better of 𝑶(N⋅log2(N)) comparisons and 𝑶(N⋅log2(K/S + S)) operations where
This results in substantially improved performance for large N;
integer_sortfloat_sort
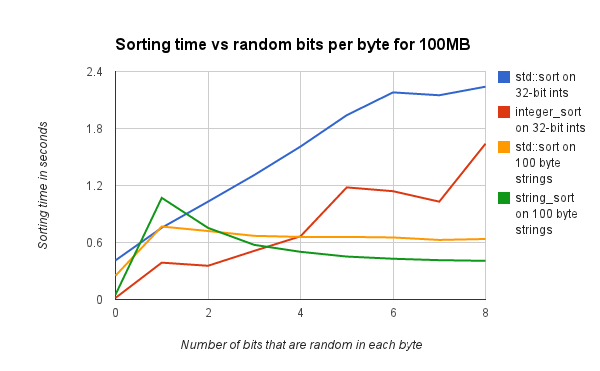
Performance graphs are provided for integer_sortfloat_sortstring_sort
Runtime Performance comparisons and graphs were made on a Core 2 Duo laptop running Windows Vista 64 with MSVC 8.0, and an old G4 laptop running Mac OSX with gcc. Boost bjam/b2 was used to control compilation.
Direct performance comparisons on a newer x86 system running Ubuntu, with the fallback to std::sort at lower input sizes disabled are below.
![[Note]](../../../../doc/src/images/note.png) |
Note |
|---|---|
The fallback to std::sort for smaller input sizes prevents the worse performance seen on the left sides of the first two graphs. |
integer_sortstring_sort
![[Note]](../../../../doc/src/images/note.png) |
Note |
|---|---|
The 4-threaded graph has 4 threads doing separate sorts simultaneously (not splitting up a single sort) as a test for thread cache collision and other multi-threaded performance issues. |
float_sortinteger_sort



Histogramming with a fixed maximum number of splits is used because it reduces the number of cache misses, thus improving performance relative to the approach described in detail in the original SpreadSort publication.
The importance of cache-friendly histogramming is described in Arne Maus, Adaptive Left Reflex, though without the worst-case handling described below.
The time taken per radix iteration is:
𝑶(N) iterations over the data
𝑶(N) integer-type comparisons (even for _float_sort and
string_sort
𝑶(N) swaps
𝑶(2S) bin operations.
To obtain 𝑶(N) worst-case performance per iteration, the restriction S <= log2(N) is applied, and 𝑶(2S) becomes 𝑶(N). For each such iteration, the number of unsorted bits log2(range) (referred to as K) per element is reduced by S. As S decreases depending upon the amount of elements being sorted, it can drop from a maximum of Smax to the minimum of Smin.
Assumption: std::sort is assumed to be 𝑶(N*log2(N)), as introsort exists and is commonly used. (If you have a quibble with this please take it up with the implementor of your std::sort; you're welcome to replace the recursive calls to std::sort to calls to introsort if your std::sort library call is poorly implemented).
Introsort is not included with this algorithm for simplicity and because the implementor of the std::sort call is assumed to know what they're doing.
To maintain a minimum value for S (Smin), comparison-based
sorting has to be used to sort when n <= log2(meanbinsize),
where log2(meanbinsize) (lbs) is a small constant, usually
between 0 and 4, used to minimize bin overhead per element. There is a small
corner-case where if K < Smin and n >=
2^K, then the data can be sorted in a single radix-based iteration
with an S = K (this bucketsorting special case is by
default only applied to float_sort
1 radix-based iteration if K <= Smin,
or Smin + lbs comparison-based iterations if K > Smin but n <= 2(Smin + lbs).
So for the final iteration, worst-case runtime is 𝑶(N*(Smin + lbs)) but if K > Smin and N > 2(Smin + lbs) then more than 1 radix recursion will be required.
For the second to last iteration, K <= Smin * 2 + 1 can be handled, (if the data is divided into 2(Smin + 1) pieces) or if N < 2(Smin + lbs + 1), then it is faster to fallback to std::sort.
In the case of a radix-based sort plus recursion, it will take 𝑶(N*(Smin + lbs)) + 𝑶(N) = 𝑶(N*(Smin + lbs + 1)) worst-case time, as K_remaining = K_start - (Smin + 1), and K_start <= Smin * 2 + 1.
Alternatively, comparison-based sorting is used if N < 2(Smin + lbs + 1), which will take 𝑶(N*(Smin + lbs + 1)) time.
So either way 𝑶(N*(Smin + lbs + 1)) is the worst-case time for the second to last iteration, which occurs if K <= Smin * 2 + 1 or N < 2(Smin + lbs + 1).
This continues as long as Smin <= S <= Smax, so that for K_m <= K_(m-1) + Smin + m where m is the maximum number of iterations after this one has finished, or where N < 2(Smin + lbs + m), then the worst-case runtime is 𝑶(N*(Smin + lbs + m)).
K_m at m <= (Smax - Smin) works out to:
K_1 <= (Smin) + Smin + 1 <= 2Smin + 1
K_2 <= (2Smin + 1) + Smin + 2
as the sum from 0 to m is m(m + 1)/2
K_m <= (m + 1)Smin + m(m + 1)/2 <= (Smin + m/2)(m + 1)
substituting in Smax - Smin for m
K_(Smax - Smin) <= (Smin + (Smax - Smin)/2)*(Smax - Smin + 1)
K_(Smax - Smin) <= (Smin + Smax) * (Smax - Smin + 1)/2
Since this involves Smax - Smin + 1 iterations, this works out to dividing K into an average (Smin + Smax)/2 pieces per iteration.
To finish the problem from this point takes 𝑶(N * (Smax - Smin)) for m iterations, plus the worst-case of 𝑶(N*(Smin + lbs)) for the last iteration, for a total of 𝑶(N *(Smax + lbs)) time.
When m > Smax - Smin, the problem is divided into Smax pieces per iteration, or std::sort is called if N < 2^(m + Smin + lbs). For this range:
K_m <= K_(m - 1) + Smax, providing runtime of
𝑶(N *((K - K_(Smax - Smin))/Smax + Smax + lbs)) if recursive,
or 𝑶(N * log(2^(m + Smin + lbs))) if comparison-based,
which simplifies to 𝑶(N * (m + Smin + lbs)), which substitutes to 𝑶(N * ((m - (Smax - Smin)) + Smax + lbs)), which given that m - (Smax - Smin) <= (K - K_(Smax - Smin))/Smax (otherwise a lesser number of radix-based iterations would be used)
also comes out to 𝑶(N *((K - K_(Smax - Smin))/Smax + Smax + lbs)).
Asymptotically, for large N and large K, this simplifies to:
𝑶(N * (K/Smax + Smax + lbs)),
simplifying out the constants related to the Smax - Smin range, providing an additional 𝑶(N * (Smax + lbs)) runtime on top of the 𝑶(N * (K/S)) performance of LSD radix sort, but without the 𝑶(N) memory overhead. For simplicity, because lbs is a small constant (0 can be used, and performs reasonably), it is ignored when summarizing the performance in further discussions. By checking whether comparison-based sorting is better, Spreadsort is also 𝑶(N*log(N)), whichever is better, and unlike LSD radix sort, can perform much better than the worst-case if the data is either evenly distributed or highly clustered.
This analysis was for integer_sortfloat_sortstring_sortstring_sort
𝑶(N * (K/Smax + (Smax comparisons))).
Worst-case, this ends up being 𝑶(N * K) (where K is the mean string length in bytes), as described for American flag sort, which is better than the
𝑶(N * K * log(N))
worst-case for comparison-based sorting.
integer_sortfloat_sortinteger_sortfloat_sort
The ideal value of max_splits depends upon the size of the L1 processor cache, and is between 10 and 13 on many systems. A default value of 11 is used. For mostly-sorted data, a much larger value is better, as swaps (and thus cache misses) are rare, but this hurts runtime severely for unsorted data, so is not recommended.
On some x86 systems, when the total number of elements being sorted is small ( less than 1 million or so), the ideal max_splits can be substantially larger, such as 17. This is suspected to be because all the data fits into the L2 cache, and misses from L1 cache to L2 cache do not impact performance as severely as misses to main memory. Modifying tuning constants other than max_splits is not recommended, as the performance improvement for changing other constants is usually minor.
If you can afford to let it run for a day, and have at least 1GB of free
memory, the perl command: ./tune.pl
-large
-tune
(UNIX) or perl tune.pl -large -tune -windows (Windows) can be used to automatically
tune these constants. This should be run from the libs/sort directory inside the boost home directory.
This will work to identify the ideal
constants.hpp settings for your system, testing on
various distributions in a 20 million element (80MB) file, and additionally
verifies that all sorting routines sort correctly across various data distributions.
Alternatively, you can test with the file size you're most concerned with
./tune.pl number
-tune
(UNIX) or perl tune.pl number
-tune
-windows
(Windows). Substitute the number of elements you want to test with for number. Otherwise, just use the options
it comes with, they're decent. With default settings ./tune.pl
-tune
(UNIX) perl tune.pl -tune -windows (Windows), the script will take
hours to run (less than a day), but may not pick the correct max_splits
if it is over 10. Alternatively, you can add the -small option to make it take just a few
minutes, tuning for smaller vector sizes (one hundred thousand elements),
but the resulting constants may not be good for large files (see above note
about max_splits on Windows).
The tuning script can also be used just to verify that sorting works correctly
on your system, and see how much of a speedup it gets, by omiting the "-tune"
option. This runs at the end of tuning runs. Default args will take about
an hour to run and give accurate results on decent-sized test vectors. ./tune.pl -small (UNIX) perl
tune.pl -small
-windows
(Windows) is a faster option, that tests on smaller vectors and isn't as
accurate.
If any differences are encountered during tuning, please call tune.pl
with -debug
> log_file_name.
If the resulting log file contains compilation or permissions issues, it
is likely an issue with your setup. If some other type of error is encountered
(or result differences), please send them to the library author at spreadsort@gmail.com.
Including the zipped input.txt that
was being used is also helpful.
Last revised: August 19, 2017 at 17:05:49 GMT |