A Boost.MPI program consists of many cooperating processes (possibly running
on different computers) that communicate among themselves by passing messages.
Boost.MPI is a library (as is the lower-level MPI), not a language, so the
first step in a Boost.MPI is to create an mpi::environment
object that initializes the MPI environment and enables communication among
the processes. The mpi::environment
object is initialized with the program arguments (which it may modify) in your
main program. The creation of this object initializes MPI, and its destruction
will finalize MPI. In the vast majority of Boost.MPI programs, an instance
of mpi::environment will
be declared in main at the
very beginning of the program.
If you run this program with 7 processes, for instance, you will receive output
such as:
Of course, the processes can execute in a different order each time, so the
ranks might not be strictly increasing. More interestingly, the text could
come out completely garbled, because one process can start writing "I
am a process" before another process has finished writing "of 7.".
If you should still have an MPI library supporting only MPI 1.1 you will need
to pass the command line arguments to the environment constructor as shown
in this example:
Point-to-Point communication
As a message passing library, MPI's primary purpose is to routine messages
from one process to another, i.e., point-to-point. MPI contains routines
that can send messages, receive messages, and query whether messages are
available. Each message has a source process, a target process, a tag, and
a payload containing arbitrary data. The source and target processes are
the ranks of the sender and receiver of the message, respectively. Tags are
integers that allow the receiver to distinguish between different messages
coming from the same sender.
The following program uses two MPI processes to write "Hello, world!"
to the screen (hello_world.cpp):
#include <boost/mpi.hpp>
#include <iostream>
#include <string>
#include <boost/serialization/string.hpp>
namespace mpi = boost::mpi;
int main()
{
mpi::environment env;
mpi::communicator world;
if (world.rank() == 0) {
world.send(1, 0, std::string("Hello"));
std::string msg;
world.recv(1, 1, msg);
std::cout << msg << "!" << std::endl;
} else {
std::string msg;
world.recv(0, 0, msg);
std::cout << msg << ", ";
std::cout.flush();
world.send(0, 1, std::string("world"));
}
return 0;
}
The first processor (rank 0) passes the message "Hello" to the
second processor (rank 1) using tag 0. The second processor prints the string
it receives, along with a comma, then passes the message "world"
back to processor 0 with a different tag. The first processor then writes
this message with the "!" and exits. All sends are accomplished
with the communicator::send
method and all receives use a corresponding communicator::recv
call.
Non-blocking communication
The default MPI communication operations--send
and recv--may have to wait
until the entire transmission is completed before they can return. Sometimes
this blocking behavior has a negative
impact on performance, because the sender could be performing useful computation
while it is waiting for the transmission to occur. More important, however,
are the cases where several communication operations must occur simultaneously,
e.g., a process will both send and receive at the same time.
Let's revisit our "Hello, world!" program from the previous section.
The core of this program transmits two messages:
if (world.rank() == 0) {
world.send(1, 0, std::string("Hello"));
std::string msg;
world.recv(1, 1, msg);
std::cout << msg << "!" << std::endl;
} else {
std::string msg;
world.recv(0, 0, msg);
std::cout << msg << ", ";
std::cout.flush();
world.send(0, 1, std::string("world"));
}
The first process passes a message to the second process, then prepares
to receive a message. The second process does the send and receive in the
opposite order. However, this sequence of events is just that--a sequence--meaning that there is essentially no parallelism.
We can use non-blocking communication to ensure that the two messages are
transmitted simultaneously (hello_world_nonblocking.cpp):
#include <boost/mpi.hpp>
#include <iostream>
#include <string>
#include <boost/serialization/string.hpp>
namespace mpi = boost::mpi;
int main()
{
mpi::environment env;
mpi::communicator world;
if (world.rank() == 0) {
mpi::request reqs[2];
std::string msg, out_msg = "Hello";
reqs[0] = world.isend(1, 0, out_msg);
reqs[1] = world.irecv(1, 1, msg);
mpi::wait_all(reqs, reqs + 2);
std::cout << msg << "!" << std::endl;
} else {
mpi::request reqs[2];
std::string msg, out_msg = "world";
reqs[0] = world.isend(0, 1, out_msg);
reqs[1] = world.irecv(0, 0, msg);
mpi::wait_all(reqs, reqs + 2);
std::cout << msg << ", ";
}
return 0;
}
We have replaced calls to the communicator::send
and communicator::recv
members with similar calls to their non-blocking counterparts, communicator::isend
and communicator::irecv.
The prefix i indicates that the operations
return immediately with a mpi::request
object, which allows one to query the status of a communication request
(see the test
method) or wait until it has completed (see the wait
method). Multiple requests can be completed at the same time with the
wait_all operation.
![[Important]](../../../doc/src/images/important.png) |
Important |
The MPI standard requires users to keep the request handle for a non-blocking
communication, and to call the "wait" operation (or successfully
test for completion) to complete the send or receive. Unlike most C MPI
implementations, which allow the user to discard the request for a non-blocking
send, Boost.MPI requires the user to call "wait" or "test",
since the request object might contain temporary buffers that have to
be kept until the send is completed. Moreover, the MPI standard does
not guarantee that the receive makes any progress before a call to "wait"
or "test", although most implementations of the C MPI do allow
receives to progress before the call to "wait" or "test".
Boost.MPI, on the other hand, generally requires "test" or
"wait" calls to make progress.
|
If you run this program multiple times, you may see some strange results:
namely, some runs will produce:
Hello, world!
while others will produce:
world!
Hello,
or even some garbled version of the letters in "Hello" and "world".
This indicates that there is some parallelism in the program, because after
both messages are (simultaneously) transmitted, both processes will concurrent
execute their print statements. For both performance and correctness, non-blocking
communication operations are critical to many parallel applications using
MPI.
The inclusion of boost/serialization/string.hpp
in the previous examples is very important: it makes values of type std::string serializable, so that they can
be be transmitted using Boost.MPI. In general, built-in C++ types (ints, floats,
characters, etc.) can be transmitted over MPI directly, while user-defined
and library-defined types will need to first be serialized (packed) into
a format that is amenable to transmission. Boost.MPI relies on the Boost.Serialization library
to serialize and deserialize data types.
For types defined by the standard library (such as std::string
or std::vector) and some types in Boost (such
as boost::variant), the Boost.Serialization
library already contains all of the required serialization code. In these
cases, you need only include the appropriate header from the boost/serialization directory.
For types that do not already have a serialization header, you will first
need to implement serialization code before the types can be transmitted
using Boost.MPI. Consider a simple class gps_position that contains members
degrees, minutes, and seconds.
This class is made serializable by making it a friend of boost::serialization::access and introducing the templated
serialize()
function, as follows:
class gps_position
{
private:
friend class boost::serialization::access;
template<class Archive>
void serialize(Archive & ar, const unsigned int version)
{
ar & degrees;
ar & minutes;
ar & seconds;
}
int degrees;
int minutes;
float seconds;
public:
gps_position(){};
gps_position(int d, int m, float s) :
degrees(d), minutes(m), seconds(s)
{}
};
Complete information about making types serializable is beyond the scope
of this tutorial. For more information, please see the Boost.Serialization
library tutorial from which the above example was extracted. One important
side benefit of making types serializable for Boost.MPI is that they become
serializable for any other usage, such as storing the objects to disk and
manipulated them in XML.
Some serializable types, like gps_position above, have a fixed
amount of data stored at fixed offsets and are fully defined by the values
of their data member (most POD with no pointers are a good example). When
this is the case, Boost.MPI can optimize their serialization and transmission
by avoiding extraneous copy operations. To enable this optimization, users
must specialize the type trait is_mpi_datatype, e.g.:
namespace boost { namespace mpi {
template <>
struct is_mpi_datatype<gps_position> : mpl::true_ { };
} }
For non-template types we have defined a macro to simplify declaring a
type as an MPI datatype
BOOST_IS_MPI_DATATYPE(gps_position)
For composite traits, the specialization of is_mpi_datatype may depend
on is_mpi_datatype itself.
For instance, a boost::array object is fixed only when the type
of the parameter it stores is fixed:
namespace boost { namespace mpi {
template <typename T, std::size_t N>
struct is_mpi_datatype<array<T, N> >
: public is_mpi_datatype<T> { };
} }
The redundant copy elimination optimization can only be applied when the
shape of the data type is completely fixed. Variable-length types (e.g.,
strings, linked lists) and types that store pointers cannot use the optimization,
but Boost.MPI will be unable to detect this error at compile time. Attempting
to perform this optimization when it is not correct will likely result
in segmentation faults and other strange program behavior.
Boost.MPI can transmit any user-defined data type from one process to another.
Built-in types can be transmitted without any extra effort; library-defined
types require the inclusion of a serialization header; and user-defined
types will require the addition of serialization code. Fixed data types
can be optimized for transmission using the is_mpi_datatype type trait.
Point-to-point operations are the
core message passing primitives in Boost.MPI. However, many message-passing
applications also require higher-level communication algorithms that combine
or summarize the data stored on many different processes. These algorithms
support many common tasks such as "broadcast this value to all processes",
"compute the sum of the values on all processors" or "find
the global minimum."
The broadcast
algorithm is by far the simplest collective operation. It broadcasts a
value from a single process to all other processes within a communicator. For instance,
the following program broadcasts "Hello, World!" from process
0 to every other process. (hello_world_broadcast.cpp)
#include <boost/mpi.hpp>
#include <iostream>
#include <string>
#include <boost/serialization/string.hpp>
namespace mpi = boost::mpi;
int main()
{
mpi::environment env;
mpi::communicator world;
std::string value;
if (world.rank() == 0) {
value = "Hello, World!";
}
broadcast(world, value, 0);
std::cout << "Process #" << world.rank() << " says " << value
<< std::endl;
return 0;
}
Running this program with seven processes will produce a result such as:
Process #0 says Hello, World!
Process #2 says Hello, World!
Process #1 says Hello, World!
Process #4 says Hello, World!
Process #3 says Hello, World!
Process #5 says Hello, World!
Process #6 says Hello, World!
The gather
collective gathers the values produced by every process in a communicator
into a vector of values on the "root" process (specified by an
argument to gather). The
/i/th element in the vector will correspond to the value gathered from
the /i/th process. For instance, in the following program each process
computes its own random number. All of these random numbers are gathered
at process 0 (the "root" in this case), which prints out the
values that correspond to each processor. (random_gather.cpp)
#include <boost/mpi.hpp>
#include <iostream>
#include <vector>
#include <cstdlib>
namespace mpi = boost::mpi;
int main()
{
mpi::environment env;
mpi::communicator world;
std::srand(time(0) + world.rank());
int my_number = std::rand();
if (world.rank() == 0) {
std::vector<int> all_numbers;
gather(world, my_number, all_numbers, 0);
for (int proc = 0; proc < world.size(); ++proc)
std::cout << "Process #" << proc << " thought of "
<< all_numbers[proc] << std::endl;
} else {
gather(world, my_number, 0);
}
return 0;
}
Executing this program with seven processes will result in output such
as the following. Although the random values will change from one run to
the next, the order of the processes in the output will remain the same
because only process 0 writes to std::cout.
Process #0 thought of 332199874
Process #1 thought of 20145617
Process #2 thought of 1862420122
Process #3 thought of 480422940
Process #4 thought of 1253380219
Process #5 thought of 949458815
Process #6 thought of 650073868
The gather operation collects
values from every process into a vector at one process. If instead the
values from every process need to be collected into identical vectors on
every process, use the all_gather algorithm,
which is semantically equivalent to calling gather
followed by a broadcast
of the resulting vector.
The scatter
collective scatters the values from a vector in the "root" process
in a communicator into values in all the processes of the communicator.
The /i/th element in the vector will correspond to the value received by
the /i/th process. For instance, in the following program, the root process
produces a vector of random nomber and send one value to each process that
will print it. (random_scatter.cpp)
#include <boost/mpi.hpp>
#include <boost/mpi/collectives.hpp>
#include <iostream>
#include <cstdlib>
#include <vector>
namespace mpi = boost::mpi;
int main(int argc, char* argv[])
{
mpi::environment env(argc, argv);
mpi::communicator world;
std::srand(time(0) + world.rank());
std::vector<int> all;
int mine = -1;
if (world.rank() == 0) {
all.resize(world.size());
std::generate(all.begin(), all.end(), std::rand);
}
mpi::scatter(world, all, mine, 0);
for (int r = 0; r < world.size(); ++r) {
world.barrier();
if (r == world.rank()) {
std::cout << "Rank " << r << " got " << mine << '\n';
}
}
return 0;
}
Executing this program with seven processes will result in output such
as the following. Although the random values will change from one run to
the next, the order of the processes in the output will remain the same
because of the barrier.
Rank 0 got 1409381269
Rank 1 got 17045268
Rank 2 got 440120016
Rank 3 got 936998224
Rank 4 got 1827129182
Rank 5 got 1951746047
Rank 6 got 2117359639
The reduce
collective summarizes the values from each process into a single value
at the user-specified "root" process. The Boost.MPI reduce operation is similar in spirit
to the STL accumulate operation, because
it takes a sequence of values (one per process) and combines them via a
function object. For instance, we can randomly generate values in each
process and the compute the minimum value over all processes via a call
to reduce
(random_min.cpp):
#include <boost/mpi.hpp>
#include <iostream>
#include <cstdlib>
namespace mpi = boost::mpi;
int main()
{
mpi::environment env;
mpi::communicator world;
std::srand(time(0) + world.rank());
int my_number = std::rand();
if (world.rank() == 0) {
int minimum;
reduce(world, my_number, minimum, mpi::minimum<int>(), 0);
std::cout << "The minimum value is " << minimum << std::endl;
} else {
reduce(world, my_number, mpi::minimum<int>(), 0);
}
return 0;
}
The use of mpi::minimum<int>
indicates that the minimum value should be computed. mpi::minimum<int> is a binary function object that compares
its two parameters via <
and returns the smaller value. Any associative binary function or function
object will work provided it's stateless. For instance, to concatenate
strings with reduce one
could use the function object std::plus<std::string> (string_cat.cpp):
#include <boost/mpi.hpp>
#include <iostream>
#include <string>
#include <functional>
#include <boost/serialization/string.hpp>
namespace mpi = boost::mpi;
int main()
{
mpi::environment env;
mpi::communicator world;
std::string names[10] = { "zero ", "one ", "two ", "three ",
"four ", "five ", "six ", "seven ",
"eight ", "nine " };
std::string result;
reduce(world,
world.rank() < 10? names[world.rank()]
: std::string("many "),
result, std::plus<std::string>(), 0);
if (world.rank() == 0)
std::cout << "The result is " << result << std::endl;
return 0;
}
In this example, we compute a string for each process and then perform
a reduction that concatenates all of the strings together into one, long
string. Executing this program with seven processors yields the following
output:
The result is zero one two three four five six
Binary operations for reduce
Any kind of binary function objects can be used with reduce.
For instance, and there are many such function objects in the C++ standard
<functional> header and the Boost.MPI header <boost/mpi/operations.hpp>. Or, you can create your own function
object. Function objects used with reduce
must be associative, i.e. f(x,
f(y, z)) must be equivalent to f(f(x, y), z). If they are also commutative (i..e,
f(x, y) == f(y,
x)),
Boost.MPI can use a more efficient implementation of reduce.
To state that a function object is commutative, you will need to specialize
the class is_commutative.
For instance, we could modify the previous example by telling Boost.MPI
that string concatenation is commutative:
namespace boost { namespace mpi {
template<>
struct is_commutative<std::plus<std::string>, std::string>
: mpl::true_ { };
} }
By adding this code prior to main(), Boost.MPI will assume that string concatenation
is commutative and employ a different parallel algorithm for the reduce operation. Using this algorithm,
the program outputs the following when run with seven processes:
The result is zero one four five six two three
Note how the numbers in the resulting string are in a different order:
this is a direct result of Boost.MPI reordering operations. The result
in this case differed from the non-commutative result because string concatenation
is not commutative: f("x",
"y")
is not the same as f("y",
"x"),
because argument order matters. For truly commutative operations (e.g.,
integer addition), the more efficient commutative algorithm will produce
the same result as the non-commutative algorithm. Boost.MPI also performs
direct mappings from function objects in <functional>
to MPI_Op values predefined
by MPI (e.g., MPI_SUM,
MPI_MAX); if you have your
own function objects that can take advantage of this mapping, see the class
template is_mpi_op.
![[Warning]](../../../doc/src/images/warning.png) |
Warning |
Due to the unerlying MPI limitations, it is important to note that the
opertation must be stateless.
|
All process variant
Like gather,
reduce has an "all"
variant called all_reduce that performs
the reduction operation and broadcasts the result to all processes. This
variant is useful, for instance, in establishing global minimum or maximum
values.
The following code (global_min.cpp)
shows a broadcasting version of the random_min.cpp
example:
#include <boost/mpi.hpp>
#include <iostream>
#include <cstdlib>
namespace mpi = boost::mpi;
int main(int argc, char* argv[])
{
mpi::environment env(argc, argv);
mpi::communicator world;
std::srand(world.rank());
int my_number = std::rand();
int minimum;
mpi::all_reduce(world, my_number, minimum, mpi::minimum<int>());
if (world.rank() == 0) {
std::cout << "The minimum value is " << minimum << std::endl;
}
return 0;
}
In that example we provide both input and output values, requiring twice
as much space, which can be a problem depending on the size of the transmitted
data. If there is no need to preserve the input value, the output value
can be omitted. In that case the input value will be overridden with the
output value and Boost.MPI is able, in some situation, to implement the
operation with a more space efficient solution (using the MPI_IN_PLACE flag of the MPI C mapping),
as in the following example (in_place_global_min.cpp):
#include <boost/mpi.hpp>
#include <iostream>
#include <cstdlib>
namespace mpi = boost::mpi;
int main(int argc, char* argv[])
{
mpi::environment env(argc, argv);
mpi::communicator world;
std::srand(world.rank());
int my_number = std::rand();
mpi::all_reduce(world, my_number, mpi::minimum<int>());
if (world.rank() == 0) {
std::cout << "The minimum value is " << my_number << std::endl;
}
return 0;
}
Communication with Boost.MPI always occurs over a communicator. A communicator
contains a set of processes that can send messages among themselves and perform
collective operations. There can be many communicators within a single program,
each of which contains its own isolated communication space that acts independently
of the other communicators.
When the MPI environment is initialized, only the "world" communicator
(called MPI_COMM_WORLD in
the MPI C and Fortran bindings) is available. The "world" communicator,
accessed by default-constructing a mpi::communicator
object, contains all of the MPI processes present when the program begins
execution. Other communicators can then be constructed by duplicating or
building subsets of the "world" communicator. For instance, in
the following program we split the processes into two groups: one for processes
generating data and the other for processes that will collect the data. (generate_collect.cpp)
#include <boost/mpi.hpp>
#include <iostream>
#include <cstdlib>
#include <boost/serialization/vector.hpp>
namespace mpi = boost::mpi;
enum message_tags {msg_data_packet, msg_broadcast_data, msg_finished};
void generate_data(mpi::communicator local, mpi::communicator world);
void collect_data(mpi::communicator local, mpi::communicator world);
int main()
{
mpi::environment env;
mpi::communicator world;
bool is_generator = world.rank() < 2 * world.size() / 3;
mpi::communicator local = world.split(is_generator? 0 : 1);
if (is_generator) generate_data(local, world);
else collect_data(local, world);
return 0;
}
When communicators are split in this way, their processes retain membership
in both the original communicator (which is not altered by the split) and
the new communicator. However, the ranks of the processes may be different
from one communicator to the next, because the rank values within a communicator
are always contiguous values starting at zero. In the example above, the
first two thirds of the processes become "generators" and the remaining
processes become "collectors". The ranks of the "collectors"
in the world communicator
will be 2/3 world.size()
and greater, whereas the ranks of the same collector processes in the local communicator will start at zero.
The following excerpt from collect_data() (in generate_collect.cpp) illustrates
how to manage multiple communicators:
mpi::status msg = world.probe();
if (msg.tag() == msg_data_packet) {
std::vector<int> data;
world.recv(msg.source(), msg.tag(), data);
for (int dest = 1; dest < local.size(); ++dest)
local.send(dest, msg_broadcast_data, msg.source());
broadcast(local, data, 0);
}
The code in this except is executed by the "master" collector,
e.g., the node with rank 2/3 world.size()
in the world communicator
and rank 0 in the local (collector)
communicator. It receives a message from a generator via the world communicator, then broadcasts the
message to each of the collectors via the local
communicator.
For more control in the creation of communicators for subgroups of processes,
the Boost.MPI group
provides facilities to compute the union (|),
intersection (&), and difference
(-) of two groups, generate
arbitrary subgroups, etc.
A communicator can be organised as a cartesian grid, here a basic example:
#include <vector>
#include <iostream>
#include <boost/mpi/communicator.hpp>
#include <boost/mpi/collectives.hpp>
#include <boost/mpi/environment.hpp>
#include <boost/mpi/cartesian_communicator.hpp>
#include <boost/test/minimal.hpp>
namespace mpi = boost::mpi;
int test_main(int argc, char* argv[])
{
mpi::environment env;
mpi::communicator world;
if (world.size() != 24) return -1;
mpi::cartesian_dimension dims[] = {{2, true}, {3,true}, {4,true}};
mpi::cartesian_communicator cart(world, mpi::cartesian_topology(dims));
for (int r = 0; r < cart.size(); ++r) {
cart.barrier();
if (r == cart.rank()) {
std::vector<int> c = cart.coordinates(r);
std::cout << "rk :" << r << " coords: "
<< c[0] << ' ' << c[1] << ' ' << c[2] << '\n';
}
}
return 0;
}
Separating structure from content
When communicating data types over MPI that are not fundamental to MPI
(such as strings, lists, and user-defined data types), Boost.MPI must first
serialize these data types into a buffer and then communicate them; the
receiver then copies the results into a buffer before deserializing into
an object on the other end. For some data types, this overhead can be eliminated
by using is_mpi_datatype.
However, variable-length data types such as strings and lists cannot be
MPI data types.
Boost.MPI supports a second technique for improving performance by separating
the structure of these variable-length data structures from the content
stored in the data structures. This feature is only beneficial when the
shape of the data structure remains the same but the content of the data
structure will need to be communicated several times. For instance, in
a finite element analysis the structure of the mesh may be fixed at the
beginning of computation but the various variables on the cells of the
mesh (temperature, stress, etc.) will be communicated many times within
the iterative analysis process. In this case, Boost.MPI allows one to first
send the "skeleton" of the mesh once, then transmit the "content"
multiple times. Since the content need not contain any information about
the structure of the data type, it can be transmitted without creating
separate communication buffers.
To illustrate the use of skeletons and content, we will take a somewhat
more limited example wherein a master process generates random number sequences
into a list and transmits them to several slave processes. The length of
the list will be fixed at program startup, so the content of the list (i.e.,
the current sequence of numbers) can be transmitted efficiently. The complete
example is available in example/random_content.cpp.
We being with the master process (rank 0), which builds a list, communicates
its structure via a skeleton, then repeatedly
generates random number sequences to be broadcast to the slave processes
via content:
std::list<int> l(list_len);
broadcast(world, mpi::skeleton(l), 0);
mpi::content c = mpi::get_content(l);
for (int i = 0; i < iterations; ++i) {
std::generate(l.begin(), l.end(), &random);
broadcast(world, c, 0);
}
std::fill(l.begin(), l.end(), 0);
broadcast(world, c, 0);
The slave processes have a very similar structure to the master. They receive
(via the broadcast() call) the skeleton of
the data structure, then use it to build their own lists of integers. In
each iteration, they receive via another broadcast() the new content in the data structure
and compute some property of the data:
std::list<int> l;
broadcast(world, mpi::skeleton(l), 0);
mpi::content c = mpi::get_content(l);
int i = 0;
do {
broadcast(world, c, 0);
if (std::find_if
(l.begin(), l.end(),
std::bind1st(std::not_equal_to<int>(), 0)) == l.end())
break;
++i;
} while (true);
The skeletons and content of any Serializable data type can be transmitted
either via the send and recv members of the communicator
class (for point-to-point communicators) or broadcast via the broadcast() collective. When separating
a data structure into a skeleton and content, be careful not to modify
the data structure (either on the sender side or the receiver side) without
transmitting the skeleton again. Boost.MPI can not detect these accidental
modifications to the data structure, which will likely result in incorrect
data being transmitted or unstable programs.
Performance optimizations
Serialization optimizations
To obtain optimal performance for small fixed-length data types not containing
any pointers it is very important to mark them using the type traits
of Boost.MPI and Boost.Serialization.
It was already discussed that fixed length types containing no pointers
can be using as is_mpi_datatype, e.g.:
namespace boost { namespace mpi {
template <>
struct is_mpi_datatype<gps_position> : mpl::true_ { };
} }
or the equivalent macro
BOOST_IS_MPI_DATATYPE(gps_position)
In addition it can give a substantial performance gain to turn off tracking
and versioning for these types, if no pointers to these types are used,
by using the traits classes or helper macros of Boost.Serialization:
BOOST_CLASS_TRACKING(gps_position,track_never)
BOOST_CLASS_IMPLEMENTATION(gps_position,object_serializable)
More optimizations are possible on homogeneous machines, by avoiding
MPI_Pack/MPI_Unpack calls but using direct bitwise copy. This feature
is enabled by default by defining the macro BOOST_MPI_HOMOGENEOUS
in the include file boost/mpi/config.hpp.
That definition must be consistent when building Boost.MPI and when building
the application.
In addition all classes need to be marked both as is_mpi_datatype and
as is_bitwise_serializable, by using the helper macro of Boost.Serialization:
BOOST_IS_BITWISE_SERIALIZABLE(gps_position)
Usually it is safe to serialize a class for which is_mpi_datatype is
true by using binary copy of the bits. The exception are classes for
which some members should be skipped for serialization.
Mapping from C MPI to Boost.MPI
This section provides tables that map from the functions and constants
of the standard C MPI to their Boost.MPI equivalents. It will be most useful
for users that are already familiar with the C or Fortran interfaces to
MPI, or for porting existing parallel programs to Boost.MPI.
Table 26.1. Point-to-point communication
Boost.MPI automatically maps C and C++ data types to their MPI equivalents.
The following table illustrates the mappings between C++ types and MPI
datatype constants.
Table 26.2. Datatypes
|
C Constant
|
Boost.MPI Equivalent
|
|
MPI_CHAR
|
signed char
|
|
MPI_SHORT
|
signed short
int
|
|
MPI_INT
|
signed int
|
|
MPI_LONG
|
signed long
int
|
|
MPI_UNSIGNED_CHAR
|
unsigned char
|
|
MPI_UNSIGNED_SHORT
|
unsigned short
int
|
|
MPI_UNSIGNED_INT
|
unsigned int
|
|
MPI_UNSIGNED_LONG
|
unsigned long
int
|
|
MPI_FLOAT
|
float
|
|
MPI_DOUBLE
|
double
|
|
MPI_LONG_DOUBLE
|
long double
|
|
MPI_BYTE
|
unused
|
|
MPI_PACKED
|
used internally for serialized
data types
|
|
MPI_LONG_LONG_INT
|
long long
int, if supported by compiler
|
|
MPI_UNSIGNED_LONG_LONG_INT
|
unsigned long
long int,
if supported by compiler
|
|
MPI_FLOAT_INT
|
std::pair<float,
int>
|
|
MPI_DOUBLE_INT
|
std::pair<double,
int>
|
|
MPI_LONG_INT
|
std::pair<long,
int>
|
|
MPI_2INT
|
std::pair<int,
int>
|
|
MPI_SHORT_INT
|
std::pair<short,
int>
|
|
MPI_LONG_DOUBLE_INT
|
std::pair<long double, int>
|
Boost.MPI does not provide direct wrappers to the MPI derived datatypes
functionality. Instead, Boost.MPI relies on the Boost.Serialization
library to construct MPI datatypes for user-defined classes. The section
on user-defined data types describes
this mechanism, which is used for types that marked as "MPI datatypes"
using is_mpi_datatype.
The derived datatypes table that follows describes which C++ types correspond
to the functionality of the C MPI's datatype constructor. Boost.MPI may
not actually use the C MPI function listed when building datatypes of a
certain form. Since the actual datatypes built by Boost.MPI are typically
hidden from the user, many of these operations are called internally by
Boost.MPI.
Table 26.3. Derived datatypes
MPI's packing facilities store values into a contiguous buffer, which can
later be transmitted via MPI and unpacked into separate values via MPI's
unpacking facilities. As with datatypes, Boost.MPI provides an abstract
interface to MPI's packing and unpacking facilities. In particular, the
two archive classes packed_oarchive and packed_iarchive
can be used to pack or unpack a contiguous buffer using MPI's facilities.
Table 26.4. Packing and unpacking
Boost.MPI supports a one-to-one mapping for most of the MPI collectives.
For each collective provided by Boost.MPI, the underlying C MPI collective
will be invoked when it is possible (and efficient) to do so.
Boost.MPI uses function objects to specify how reductions should occur
in its equivalents to MPI_Allreduce,
MPI_Reduce, and MPI_Scan. The following table illustrates
how predefined
and user-defined
reduction operations can be mapped between the C MPI and Boost.MPI.
Table 26.6. Reduction operations
|
C Constant
|
Boost.MPI Equivalent
|
|
MPI_BAND
|
bitwise_and
|
|
MPI_BOR
|
bitwise_or
|
|
MPI_BXOR
|
bitwise_xor
|
|
MPI_LAND
|
std::logical_and
|
|
MPI_LOR
|
std::logical_or
|
|
MPI_LXOR
|
logical_xor
|
|
MPI_MAX
|
maximum
|
|
MPI_MAXLOC
|
unsupported
|
|
MPI_MIN
|
minimum
|
|
MPI_MINLOC
|
unsupported
|
|
MPI_Op_create
|
used internally by Boost.MPI
|
|
MPI_Op_free
|
used internally by Boost.MPI
|
|
MPI_PROD
|
std::multiplies
|
|
MPI_SUM
|
std::plus
|
MPI defines several special communicators, including MPI_COMM_WORLD
(including all processes that the local process can communicate with),
MPI_COMM_SELF (including
only the local process), and MPI_COMM_EMPTY
(including no processes). These special communicators are all instances
of the communicator
class in Boost.MPI.
Table 26.7. Predefined communicators
|
C Constant
|
Boost.MPI Equivalent
|
|
MPI_COMM_WORLD
|
a default-constructed communicator
|
|
MPI_COMM_SELF
|
a communicator
that contains only the current process
|
|
MPI_COMM_EMPTY
|
a communicator
that evaluates false
|
Boost.MPI supports groups of processes through its group class.
Table 26.8. Group operations and constants
Boost.MPI provides manipulation of communicators through the communicator
class.
Table 26.9. Communicator operations
Boost.MPI currently provides support for inter-communicators via the intercommunicator
class.
Table 26.10. Inter-communicator operations
Boost.MPI currently provides no support for attribute caching.
Table 26.11. Attributes and caching
Boost.MPI will provide complete support for creating communicators with
different topologies and later querying those topologies. Support for graph
topologies is provided via an interface to the Boost
Graph Library (BGL), where a communicator can be created which
matches the structure of any BGL graph, and the graph topology of a communicator
can be viewed as a BGL graph for use in existing, generic graph algorithms.
Table 26.12. Process topologies
Boost.MPI supports environmental inquires through the environment class.
Table 26.13. Environmental inquiries
Boost.MPI translates MPI errors into exceptions, reported via the exception
class.
Table 26.14. Error handling
The MPI timing facilities are exposed via the Boost.MPI timer class, which provides
an interface compatible with the Boost
Timer library.
Table 26.15. Timing facilities
MPI startup and shutdown are managed by the construction and destruction
of the Boost.MPI environment class.
Table 26.16. Startup/shutdown facilities
Boost.MPI does not provide any support for the profiling facilities in
MPI 1.1.
Table 26.17. Profiling interface
This file is a top-level convenience header that includes all of the Boost.MPI library headers. Users concerned about compile time may wish to include only specific headers from the Boost.MPI library.
This header provides an STL-compliant allocator that uses the MPI-2 memory allocation facilities.
namespace boost {
namespace mpi {
template<typename T> class allocator;
template<> class allocator<void>;
template<typename T1, typename T2>
bool operator==(const allocator< T1 > &, const allocator< T2 > &);
template<typename T1, typename T2>
bool operator!=(const allocator< T1 > &, const allocator< T2 > &);
}
}
This header defines facilities to support MPI communicators with cartesian topologies. If known at compiled time, the dimension of the implied grid can be statically enforced, through the templatized communicator class. Otherwise, a non template, dynamic, base class is provided.
namespace boost {
namespace mpi {
class cartesian_communicator;
struct cartesian_dimension;
class cartesian_topology;
template<> struct is_mpi_datatype<cartesian_dimension>;
bool operator==(cartesian_dimension const & d1,
cartesian_dimension const & d2);
bool operator!=(cartesian_dimension const & d1,
cartesian_dimension const & d2);
std::ostream &
operator<<(std::ostream & out, cartesian_dimension const & d);
bool operator==(cartesian_topology const & t1,
cartesian_topology const & t2);
bool operator!=(cartesian_topology const & t1,
cartesian_topology const & t2);
std::ostream &
operator<<(std::ostream & out, cartesian_topology const & t);
std::vector< int > & cartesian_dimensions(int, std::vector< int > &);
}
}
This header contains MPI collective operations, which implement various parallel algorithms that require the coordination of all processes within a communicator. The header collectives_fwd.hpp provides forward declarations for each of these operations. To include only specific collective algorithms, use the headers boost/mpi/collectives/algorithm_name.hpp.
namespace boost {
namespace mpi {
template<typename T>
void all_gather(const communicator &, const T &, std::vector< T > &);
template<typename T> void all_gather(const communicator &, const T &, T *);
template<typename T>
void all_gather(const communicator &, const T *, int,
std::vector< T > &);
template<typename T>
void all_gather(const communicator &, const T *, int, T *);
template<typename T, typename Op>
void all_reduce(const communicator &, const T *, int, T *, Op);
template<typename T, typename Op>
void all_reduce(const communicator &, const T &, T &, Op);
template<typename T, typename Op>
T all_reduce(const communicator &, const T &, Op);
template<typename T, typename Op>
void all_reduce(const communicator &, inplace_t< T * >, int, Op);
template<typename T, typename Op>
void all_reduce(const communicator &, inplace_t< T >, Op);
template<typename T>
void all_to_all(const communicator &, const std::vector< T > &,
std::vector< T > &);
template<typename T> void all_to_all(const communicator &, const T *, T *);
template<typename T>
void all_to_all(const communicator &, const std::vector< T > &, int,
std::vector< T > &);
template<typename T>
void all_to_all(const communicator &, const T *, int, T *);
template<typename T> void broadcast(const communicator &, T &, int);
template<typename T> void broadcast(const communicator &, T *, int, int);
template<typename T>
void broadcast(const communicator &, skeleton_proxy< T > &, int);
template<typename T>
void broadcast(const communicator &, const skeleton_proxy< T > &, int);
template<typename T>
void gather(const communicator &, const T &, std::vector< T > &, int);
template<typename T>
void gather(const communicator &, const T &, T *, int);
template<typename T> void gather(const communicator &, const T &, int);
template<typename T>
void gather(const communicator &, const T *, int, std::vector< T > &,
int);
template<typename T>
void gather(const communicator &, const T *, int, T *, int);
template<typename T>
void gather(const communicator &, const T *, int, int);
template<typename T>
void gatherv(const communicator &, const std::vector< T > &, T *,
const std::vector< int > &, const std::vector< int > &,
int);
template<typename T>
void gatherv(const communicator &, const T *, int, T *,
const std::vector< int > &, const std::vector< int > &,
int);
template<typename T>
void gatherv(const communicator &, const std::vector< T > &, int);
template<typename T>
void gatherv(const communicator &, const T *, int, int);
template<typename T>
void gatherv(const communicator &, const T *, int, T *,
const std::vector< int > &, int);
template<typename T>
void gatherv(const communicator &, const std::vector< T > &, T *,
const std::vector< int > &, int);
template<typename T>
void scatter(const communicator &, const std::vector< T > &, T &, int);
template<typename T>
void scatter(const communicator &, const T *, T &, int);
template<typename T> void scatter(const communicator &, T &, int);
template<typename T>
void scatter(const communicator &, const std::vector< T > &, T *, int,
int);
template<typename T>
void scatter(const communicator &, const T *, T *, int, int);
template<typename T> void scatter(const communicator &, T *, int, int);
template<typename T>
void scatterv(const communicator &, const std::vector< T > &,
const std::vector< int > &, const std::vector< int > &,
T *, int, int);
template<typename T>
void scatterv(const communicator &, const T *,
const std::vector< int > &, const std::vector< int > &,
T *, int, int);
template<typename T> void scatterv(const communicator &, T *, int, int);
template<typename T>
void scatterv(const communicator &, const T *,
const std::vector< int > &, T *, int);
template<typename T>
void scatterv(const communicator &, const std::vector< T > &,
const std::vector< int > &, T *, int);
template<typename T, typename Op>
void reduce(const communicator &, const T &, T &, Op, int);
template<typename T, typename Op>
void reduce(const communicator &, const T &, Op, int);
template<typename T, typename Op>
void reduce(const communicator &, const T *, int, T *, Op, int);
template<typename T, typename Op>
void reduce(const communicator &, const T *, int, Op, int);
template<typename T, typename Op>
void scan(const communicator &, const T &, T &, Op);
template<typename T, typename Op>
T scan(const communicator &, const T &, Op);
template<typename T, typename Op>
void scan(const communicator &, const T *, int, T *, Op);
}
}
This header provides forward declarations for all of the collective operations contained in the header collectives.hpp.
This header provides forward declarations for the contents of the header datatype.hpp. It is expected to be used primarily by user-defined C++ classes that need to specialize is_mpi_datatype.
namespace boost {
namespace mpi {
struct packed;
template<typename T> MPI_Datatype get_mpi_datatype();
}
}
This header provides the environment class, which provides routines to initialize, finalization, and query the status of the Boost MPI environment.
namespace boost {
namespace mpi {
class environment;
namespace threading {
enum level;
std::ostream & operator<<(std::ostream &, level);
std::istream & operator>>(std::istream &, level &);
}
}
}
This header provides exception classes that report MPI errors to the user and macros that translate MPI error codes into Boost.MPI exceptions.
BOOST_MPI_CHECK_RESULT(MPIFunc, Args)
namespace boost {
namespace mpi {
class exception;
}
}
This header defines facilities to support MPI communicators with graph topologies, using the graph interface defined by the Boost Graph Library. One can construct a communicator whose topology is described by any graph meeting the requirements of the Boost Graph Library's graph concepts. Likewise, any communicator that has a graph topology can be viewed as a graph by the Boost Graph Library, permitting one to use the BGL's graph algorithms on the process topology.
namespace boost {
template<> struct graph_traits<mpi::graph_communicator>;
namespace mpi {
class graph_communicator;
int source(const std::pair< int, int > & edge, const graph_communicator &);
int target(const std::pair< int, int > & edge, const graph_communicator &);
unspecified out_edges(int vertex, const graph_communicator & comm);
int out_degree(int vertex, const graph_communicator & comm);
unspecified adjacent_vertices(int vertex, const graph_communicator & comm);
std::pair< counting_iterator< int >, counting_iterator< int > >
vertices(const graph_communicator & comm);
int num_vertices(const graph_communicator & comm);
unspecified edges(const graph_communicator & comm);
int num_edges(const graph_communicator & comm);
identity_property_map get(vertex_index_t, const graph_communicator &);
int get(vertex_index_t, const graph_communicator &, int);
}
}
This header provides helpers to indicate to MPI collective operation that a buffer can be use both as an input and output.
namespace boost {
namespace mpi {
template<typename T> struct inplace_t;
template<typename T> struct inplace_t<T *>;
template<typename T> inplace_t< T > inplace(T &);
template<typename T> inplace_t< T * > inplace(T *);
}
}
This header defines the intercommunicator class, which permits communication between different process groups.
namespace boost {
namespace mpi {
class intercommunicator;
}
}
This header defines operations for completing non-blocking communication requests.
namespace boost {
namespace mpi {
template<typename ForwardIterator>
std::pair< status, ForwardIterator >
wait_any(ForwardIterator, ForwardIterator);
template<typename ForwardIterator>
optional< std::pair< status, ForwardIterator > >
test_any(ForwardIterator, ForwardIterator);
template<typename ForwardIterator, typename OutputIterator>
OutputIterator
wait_all(ForwardIterator, ForwardIterator, OutputIterator);
template<typename ForwardIterator>
void wait_all(ForwardIterator, ForwardIterator);
template<typename ForwardIterator, typename OutputIterator>
optional< OutputIterator >
test_all(ForwardIterator, ForwardIterator, OutputIterator);
template<typename ForwardIterator>
bool test_all(ForwardIterator, ForwardIterator);
template<typename BidirectionalIterator, typename OutputIterator>
std::pair< OutputIterator, BidirectionalIterator >
wait_some(BidirectionalIterator, BidirectionalIterator, OutputIterator);
template<typename BidirectionalIterator>
BidirectionalIterator
wait_some(BidirectionalIterator, BidirectionalIterator);
template<typename BidirectionalIterator, typename OutputIterator>
std::pair< OutputIterator, BidirectionalIterator >
test_some(BidirectionalIterator, BidirectionalIterator, OutputIterator);
template<typename BidirectionalIterator>
BidirectionalIterator
test_some(BidirectionalIterator, BidirectionalIterator);
}
}
This header provides a mapping from function objects to MPI_Op constants used in MPI collective operations. It also provides several new function object types not present in the standard MPI_Op.
namespace boost {
namespace mpi {
template<typename T> struct bitwise_and;
template<typename T> struct bitwise_or;
template<typename T> struct bitwise_xor;
template<typename Op, typename T> struct is_commutative;
template<typename Op, typename T> struct is_mpi_op;
template<typename T> struct logical_xor;
template<typename T> struct maximum;
template<typename T> struct minimum;
}
}
This header provides the facilities for packing Serializable data types into a buffer using MPI_Pack. The buffers can then be transmitted via MPI and then be unpacked either via the facilities in packed_oarchive.hpp or MPI_Unpack.
namespace boost {
namespace mpi {
class packed_iarchive;
typedef packed_iprimitive iprimitive;
}
}
This header provides the facilities for unpacking Serializable data types from a buffer using MPI_Unpack. The buffers are typically received via MPI and have been packed either by via the facilities in packed_iarchive.hpp or MPI_Pack.
namespace boost {
namespace mpi {
class packed_oarchive;
typedef packed_oprimitive oprimitive;
}
}
This header interacts with the Python bindings for Boost.MPI. The routines in this header can be used to register user-defined and library-defined data types with Boost.MPI for efficient (de-)serialization and separate transmission of skeletons and content.
namespace boost {
namespace mpi {
namespace python {
template<typename T>
void register_serialized(const T & = T(), PyTypeObject * = 0);
template<typename T>
void register_skeleton_and_content(const T & = T(),
PyTypeObject * = 0);
}
}
}
This header defines the class request, which contains a request for non-blocking communication.
namespace boost {
namespace mpi {
class request;
}
}
This header provides facilities that allow the structure of data types (called the "skeleton") to be transmitted and received separately from the content stored in those data types. These facilities are useful when the data in a stable data structure (e.g., a mesh or a graph) will need to be transmitted repeatedly. In this case, transmitting the skeleton only once saves both communication effort (it need not be sent again) and local computation (serialization need only be performed once for the content).
namespace boost {
namespace mpi {
class content;
class packed_skeleton_iarchive;
class packed_skeleton_oarchive;
template<typename T> struct skeleton_proxy;
template<typename T> const skeleton_proxy< T > skeleton(T &);
template<typename T> const content get_content(const T &);
}
}
This header contains all of the forward declarations required to use transmit skeletons of data structures and the content of data structures separately. To actually transmit skeletons or content, include the header boost/mpi/skeleton_and_content.hpp.
This header defines the class status, which reports on the results of point-to-point communication.
namespace boost {
namespace mpi {
class status;
}
}
This header provides the timer class, which provides access to the MPI timers.
namespace boost {
namespace mpi {
class timer;
}
}
Boost.MPI provides an alternative MPI interface from the Python
programming language via the boost.mpi module.
The Boost.MPI Python bindings, built on top of the C++ Boost.MPI using the
Boost.Python library,
provide nearly all of the functionality of Boost.MPI within a dynamic, object-oriented
language.
The Boost.MPI Python module can be built and installed from the libs/mpi/build
directory. Just follow the configuration
and installation instructions for
the C++ Boost.MPI. Once you have installed the Python module, be sure that
the installation location is in your PYTHONPATH.
Getting started with the Boost.MPI Python module is as easy as importing
boost.mpi. Our first "Hello, World!"
program is just two lines long:
import boost.mpi as mpi
print "I am process %d of %d." % (mpi.rank, mpi.size)
Go ahead and run this program with several processes. Be sure to invoke
the python interpreter
from mpirun, e.g.,
mpirun -np 5 python hello_world.py
This will return output such as:
I am process 1 of 5.
I am process 3 of 5.
I am process 2 of 5.
I am process 4 of 5.
I am process 0 of 5.
Point-to-point operations in Boost.MPI have nearly the same syntax in Python
as in C++. We can write a simple two-process Python program that prints
"Hello, world!" by transmitting Python strings:
import boost.mpi as mpi
if mpi.world.rank == 0:
mpi.world.send(1, 0, 'Hello')
msg = mpi.world.recv(1, 1)
print msg,'!'
else:
msg = mpi.world.recv(0, 0)
print (msg + ', '),
mpi.world.send(0, 1, 'world')
There are only a few notable differences between this Python code and the
example in the C++ tutorial.
First of all, we don't need to write any initialization code in Python:
just loading the boost.mpi
module makes the appropriate MPI_Init
and MPI_Finalize calls.
Second, we're passing Python objects from one process to another through
MPI. Any Python object that can be pickled can be transmitted; the next
section will describe in more detail how the Boost.MPI Python layer transmits
objects. Finally, when we receive objects with recv,
we don't need to specify the type because transmission of Python objects
is polymorphic.
When experimenting with Boost.MPI in Python, don't forget that help is
always available via pydoc:
just pass the name of the module or module entity on the command line (e.g.,
pydoc boost.mpi.communicator)
to receive complete reference documentation. When in doubt, try it!
Transmitting User-Defined Data
Boost.MPI can transmit user-defined data in several different ways. Most
importantly, it can transmit arbitrary Python
objects by pickling them at the sender and unpickling them at the receiver,
allowing arbitrarily complex Python data structures to interoperate with
MPI.
Boost.MPI also supports efficient serialization and transmission of C++
objects (that have been exposed to Python) through its C++ interface. Any
C++ type that provides (de-)serialization routines that meet the requirements
of the Boost.Serialization library is eligible for this optimization, but
the type must be registered in advance. To register a C++ type, invoke
the C++ function register_serialized.
If your C++ types come from other Python modules (they probably will!),
those modules will need to link against the boost_mpi
and boost_mpi_python libraries
as described in the installation section.
Note that you do not need to link against
the Boost.MPI Python extension module.
Finally, Boost.MPI supports separation of the structure of an object from
the data it stores, allowing the two pieces to be transmitted separately.
This "skeleton/content" mechanism, described in more detail in
a later section, is a communication optimization suitable for problems
with fixed data structures whose internal data changes frequently.
Boost.MPI supports all of the MPI collectives (scatter,
reduce, scan,
broadcast, etc.) for any
type of data that can be transmitted with the point-to-point communication
operations. For the MPI collectives that require a user-specified operation
(e.g., reduce and scan), the operation can be an arbitrary
Python function. For instance, one could concatenate strings with all_reduce:
mpi.all_reduce(my_string, lambda x,y: x + y)
The following module-level functions implement MPI collectives: all_gather
Gather the values from all processes. all_reduce Combine the results from
all processes. all_to_all Every process sends data to every other process.
broadcast Broadcast data from one process to all other processes. gather
Gather the values from all processes to the root. reduce Combine the results
from all processes to the root. scan Prefix reduction of the values from
all processes. scatter Scatter the values stored at the root to all processes.
Skeleton/Content Mechanism
Boost.MPI provides a skeleton/content mechanism that allows the transfer
of large data structures to be split into two separate stages, with the
skeleton (or, "shape") of the data structure sent first and the
content (or, "data") of the data structure sent later, potentially
several times, so long as the structure has not changed since the skeleton
was transferred. The skeleton/content mechanism can improve performance
when the data structure is large and its shape is fixed, because while
the skeleton requires serialization (it has an unknown size), the content
transfer is fixed-size and can be done without extra copies.
To use the skeleton/content mechanism from Python, you must first register
the type of your data structure with the skeleton/content mechanism from C++. The registration function is register_skeleton_and_content
and resides in the <boost/mpi/python.hpp>
header.
Once you have registered your C++ data structures, you can extract the
skeleton for an instance of that data structure with skeleton(). The resulting skeleton_proxy
can be transmitted via the normal send routine, e.g.,
mpi.world.send(1, 0, skeleton(my_data_structure))
skeleton_proxy objects
can be received on the other end via recv(), which stores a newly-created instance
of your data structure with the same "shape" as the sender in
its "object" attribute:
shape = mpi.world.recv(0, 0)
my_data_structure = shape.object
Once the skeleton has been transmitted, the content (accessed via get_content) can be transmitted in much
the same way. Note, however, that the receiver also specifies get_content(my_data_structure)
in its call to receive:
if mpi.rank == 0:
mpi.world.send(1, 0, get_content(my_data_structure))
else:
mpi.world.recv(0, 0, get_content(my_data_structure))
Of course, this transmission of content can occur repeatedly, if the values
in the data structure--but not its shape--changes.
The skeleton/content mechanism is a structured way to exploit the interaction
between custom-built MPI datatypes and MPI_BOTTOM,
to eliminate extra buffer copies.
C++/Python MPI Compatibility
Boost.MPI is a C++ library whose facilities have been exposed to Python
via the Boost.Python library. Since the Boost.MPI Python bindings are
build directly on top of the C++ library, and nearly every feature of
C++ library is available in Python, hybrid C++/Python programs using
Boost.MPI can interact, e.g., sending a value from Python but receiving
that value in C++ (or vice versa). However, doing so requires some care.
Because Python objects are dynamically typed, Boost.MPI transfers type
information along with the serialized form of the object, so that the
object can be received even when its type is not known. This mechanism
differs from its C++ counterpart, where the static types of transmitted
values are always known.
The only way to communicate between the C++ and Python views on Boost.MPI
is to traffic entirely in Python objects. For Python, this is the normal
state of affairs, so nothing will change. For C++, this means sending
and receiving values of type boost::python::object,
from the Boost.Python
library. For instance, say we want to transmit an integer value from
Python:
comm.send(1, 0, 17)
In C++, we would receive that value into a Python object and then extract an integer value:
boost::python::object value;
comm.recv(0, 0, value);
int int_value = boost::python::extract<int>(value);
In the future, Boost.MPI will be extended to allow improved interoperability
with the C++ Boost.MPI and the C MPI bindings.
The Boost.MPI Python module, boost.mpi,
has its own reference documentation,
which is also available using pydoc
(from the command line) or help(boost.mpi) (from the Python interpreter).
The design philosophy of the Parallel MPI library is very simple: be both
convenient and efficient. MPI is a library built for high-performance applications,
but it's FORTRAN-centric, performance-minded design makes it rather inflexible
from the C++ point of view: passing a string from one process to another
is inconvenient, requiring several messages and explicit buffering; passing
a container of strings from one process to another requires an extra level
of manual bookkeeping; and passing a map from strings to containers of
strings is positively infuriating. The Parallel MPI library allows all
of these data types to be passed using the same simple send() and recv() primitives. Likewise, collective operations
such as reduce() allow arbitrary data types
and function objects, much like the C++ Standard Library would.
The higher-level abstractions provided for convenience must not have an
impact on the performance of the application. For instance, sending an
integer via send must be
as efficient as a call to MPI_Send,
which means that it must be implemented by a simple call to MPI_Send; likewise, an integer reduce() using std::plus<int> must be implemented with a call to
MPI_Reduce on integers
using the MPI_SUM operation:
anything less will impact performance. In essence, this is the "don't
pay for what you don't use" principle: if the user is not transmitting
strings, s/he should not pay the overhead associated with strings.
Sometimes, achieving maximal performance means foregoing convenient abstractions
and implementing certain functionality using lower-level primitives. For
this reason, it is always possible to extract enough information from the
abstractions in Boost.MPI to minimize the amount of effort required to
interface between Boost.MPI and the C MPI library.
There are an increasing number of hybrid parallel applications that mix
distributed and shared memory parallelism. To know how to support that
model, one need to know what level of threading support is guaranteed by
the MPI implementation. There are 4 ordered level of possible threading
support described by mpi::threading::level.
At the lowest level, you should not use threads at all, at the highest
level, any thread can perform MPI call.
If you want to use multi-threading in your MPI application, you should
indicate in the environment constructor your preferred threading support.
Then probe the one the library did provide, and decide what you can do
with it (it could be nothing, then aborting is a valid option):
#include <boost/mpi/environment.hpp>
#include <boost/mpi/communicator.hpp>
#include <iostream>
namespace mpi = boost::mpi;
namespace mt = mpi::threading;
int main()
{
mpi::environment env(mt::funneled);
if (env.thread_level() < mt::funneled) {
env.abort(-1);
}
mpi::communicator world;
std::cout << "I am process " << world.rank() << " of " << world.size()
<< "." << std::endl;
return 0;
}
Message-passing performance is crucial in high-performance distributed
computing. To evaluate the performance of Boost.MPI, we modified the standard
NetPIPE benchmark
(version 3.6.2) to use Boost.MPI and compared its performance against raw
MPI. We ran five different variants of the NetPIPE benchmark:
-
MPI: The unmodified NetPIPE benchmark.
-
Boost.MPI: NetPIPE modified to use Boost.MPI calls for communication.
-
MPI (Datatypes): NetPIPE modified to use a derived datatype (which
itself contains a single
MPI_BYTE)
rather than a fundamental datatype.
-
Boost.MPI (Datatypes): NetPIPE modified to use a user-defined type
Char in place of the
fundamental char type.
The Char type contains
a single char, a serialize()
method to make it serializable, and specializes is_mpi_datatype
to force Boost.MPI to build a derived MPI data type for it.
-
Boost.MPI (Serialized): NetPIPE modified to use a user-defined type
Char in place of the
fundamental char type.
This Char type contains
a single char and is serializable.
Unlike the Datatypes case, is_mpi_datatype
is not specialized, forcing Boost.MPI
to perform many, many serialization calls.
The actual tests were performed on the Odin cluster in the Department
of Computer Science at Indiana
University, which contains 128 nodes connected via Infiniband.
Each node contains 4GB memory and two AMD Opteron processors. The NetPIPE
benchmarks were compiled with Intel's C++ Compiler, version 9.0, Boost
1.35.0 (prerelease), and Open MPI
version 1.1. The NetPIPE results follow:
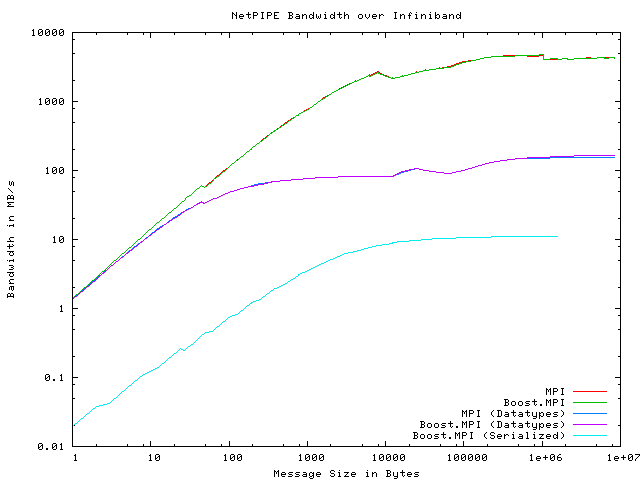
There are a some observations we can make about these NetPIPE results.
First of all, the top two plots show that Boost.MPI performs on par with
MPI for fundamental types. The next two plots show that Boost.MPI performs
on par with MPI for derived data types, even though Boost.MPI provides
a much more abstract, completely transparent approach to building derived
data types than raw MPI. Overall performance for derived data types is
significantly worse than for fundamental data types, but the bottleneck
is in the underlying MPI implementation itself. Finally, when forcing Boost.MPI
to serialize characters individually, performance suffers greatly. This
particular instance is the worst possible case for Boost.MPI, because we
are serializing millions of individual characters. Overall, the additional
abstraction provided by Boost.MPI does not impair its performance.
-
Boost 1.36.0:
-
Support for non-blocking operations in Python, from Andreas Klöckner
-
Boost 1.35.0: Initial release, containing
the following post-review changes
-
Support for arrays in all collective operations
-
Support default-construction of
environment
-
2006-09-21: Boost.MPI accepted into
Boost.
Boost.MPI was developed with support from Zurcher Kantonalbank. Daniel
Egloff and Michael Gauckler contributed many ideas to Boost.MPI's design,
particularly in the design of its abstractions for MPI data types and the
novel skeleton/context mechanism for large data structures. Prabhanjan
(Anju) Kambadur developed the predecessor to Boost.MPI that proved the
usefulness of the Serialization library in an MPI setting and the performance
benefits of specialization in a C++ abstraction layer for MPI. Jeremy Siek
managed the formal review of Boost.MPI.
 Boost
C++ Libraries
Boost
C++ Libraries



![[Important]](../../../doc/src/images/important.png)
![[Warning]](../../../doc/src/images/warning.png)
