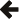#include <boost/multiprecision/cpp_int.hpp>
namespace boost{ namespace multiprecision{
typedef unspecified-type limb_type;
enum cpp_integer_type { signed_magnitude, unsigned_magnitude };
enum cpp_int_check_type { checked, unchecked };
template <unsigned MinBits = 0,
unsigned MaxBits = 0,
cpp_integer_type SignType = signed_magnitude,
cpp_int_check_type Checked = unchecked,
class Allocator = std::allocator<limb_type> >
class cpp_int_backend;
template <unsigned MinBits, unsigned MaxBits, cpp_integer_type SignType, cpp_int_check_type Checked>
struct expression_template_default<cpp_int_backend<MinBits, MaxBits, SignType, Checked, void> >
{ static const expression_template_option value = et_off; };
typedef number<cpp_int_backend<> > cpp_int;
typedef rational_adaptor<cpp_int_backend<> > cpp_rational_backend;
typedef number<cpp_rational_backend> cpp_rational;
typedef number<cpp_int_backend<128, 128, unsigned_magnitude, unchecked, void> > uint128_t;
typedef number<cpp_int_backend<256, 256, unsigned_magnitude, unchecked, void> > uint256_t;
typedef number<cpp_int_backend<512, 512, unsigned_magnitude, unchecked, void> > uint512_t;
typedef number<cpp_int_backend<1024, 1024, unsigned_magnitude, unchecked, void> > uint1024_t;
typedef number<cpp_int_backend<128, 128, signed_magnitude, unchecked, void> > int128_t;
typedef number<cpp_int_backend<256, 256, signed_magnitude, unchecked, void> > int256_t;
typedef number<cpp_int_backend<512, 512, signed_magnitude, unchecked, void> > int512_t;
typedef number<cpp_int_backend<1024, 1024, signed_magnitude, unchecked, void> > int1024_t;
typedef number<cpp_int_backend<0, 0, signed_magnitude, checked> > checked_cpp_int;
typedef rational_adaptor<cpp_int_backend<0, 0, signed_magnitude, checked> > checked_cpp_rational_backend;
typedef number<cpp_rational_backend> checked_cpp_rational;
typedef number<cpp_int_backend<128, 128, unsigned_magnitude, checked, void> > checked_uint128_t;
typedef number<cpp_int_backend<256, 256, unsigned_magnitude, checked, void> > checked_uint256_t;
typedef number<cpp_int_backend<512, 512, unsigned_magnitude, checked, void> > checked_uint512_t;
typedef number<cpp_int_backend<1024, 1024, unsigned_magnitude, checked, void> > checked_uint1024_t;
typedef number<cpp_int_backend<128, 128, signed_magnitude, checked, void> > checked_int128_t;
typedef number<cpp_int_backend<256, 256, signed_magnitude, checked, void> > checked_int256_t;
typedef number<cpp_int_backend<512, 512, signed_magnitude, checked, void> > checked_int512_t;
typedef number<cpp_int_backend<1024, 1024, signed_magnitude, checked, void> > checked_int1024_t;
}}
The cpp_int_backend type
is normally used via one of the convenience typedefs given above.
This back-end is the "Swiss Army Knife" of integer types as it
can represent both fixed and arbitrary
precision integer types, and both signed and unsigned types. There
are five template arguments:
- MinBits
Determines the number of Bits to store directly within the object
before resorting to dynamic memory allocation. When zero, this field
is determined automatically based on how many bits can be stored
in union with the dynamic storage header: setting a larger value
may improve performance as larger integer values will be stored internally
before memory allocation is required.
- MaxBits
Determines the maximum number of bits to be stored in the type: resulting
in a fixed precision type. When this value is the same as MinBits,
then the Allocator parameter is ignored, as no dynamic memory allocation
will ever be performed: in this situation the Allocator parameter
should be set to type void.
Note that this parameter should not be used simply to prevent large
memory allocations, not only is that role better performed by the
allocator, but fixed precision integers have a tendency to allocate
all of MaxBits of storage more often than one would expect.
- SignType
Determines whether the resulting type is signed or not. Note that
for arbitrary
precision types this parameter must be signed_magnitude.
For fixed precision types then this type may be either signed_magnitude or unsigned_magnitude.
- Checked
This parameter has two values: checked
or unchecked. See
below.
- Allocator
The allocator to use for dynamic memory allocation, or type void if MaxBits == MinBits.
When the template parameter Checked is set to checked
then the result is a checked-integer, checked and
unchecked integers have the following properties:
Things you should know when using this type:
-
Default constructed
cpp_int_backends
have the value zero.
-
Division by zero results in a
std::overflow_error
being thrown.
-
Construction from a string that contains invalid non-numeric characters
results in a
std::runtime_error being thrown.
-
Since the precision of
cpp_int_backend
is necessarily limited when the allocator parameter is void, care should
be taken to avoid numeric overflow when using this type unless you
actually want modulo-arithmetic behavior.
-
The type uses a sign-magnitude representation internally, so type
int128_t has 128-bits
of precision plus an extra sign bit. In this respect the behaviour
of these types differs from built-in 2's complement types. In might
be tempting to use a 127-bit type instead, and indeed this does work,
but behaviour is still slightly different from a 2's complement built-in
type as the min and max values are identical (apart from the sign),
where as they differ by one for a true 2's complement type. That said
it should be noted that there's no requirement for built-in types to
be 2's complement either - it's simply that this is the most common
format by far.
-
Attempting to print negative values as either an Octal or Hexadecimal
string results in a
std::runtime_error
being thrown, this is a direct consequence of the sign-magnitude representation.
-
The fixed precision types
[checked_][u]intXXX_t have expression template
support turned off - it seems to make little difference to the performance
of these types either way - so we may as well have the faster compile
times by turning the feature off.
-
Unsigned types support subtraction - the result is "as if"
a 2's complement operation had been performed as long as they are not
checked-integers (see above). In other words they
behave pretty much as a built in integer type would in this situation.
So for example if we were using
uint128_t
then uint128_t(1)-4
would result in the value 0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFD
of type uint128_t.
However, had this operation been performed on checked_uint128_t
then a std::range_error would have been thrown.
-
Unary negation of unsigned types results in a compiler error (static
assertion).
-
This backend supports rvalue-references and is move-aware, making instantiations
of
number on this backend
move aware.
-
When used at fixed precision, the size of this type is always one machine
word (plus any compiler-applied alignment padding) larger than you
would expect for an N-bit integer: the extra word stores both the sign,
and how many machine words in the integer are actually in use. The
latter is an optimisation for larger fixed precision integers, so that
a 1024-bit integer has almost the same performance characteristics
as a 128-bit integer, rather than being 4 times slower for addition
and 16 times slower for multiplication (assuming the values involved
would always fit in 128 bits). Typically this means you can use an
integer type wide enough for the "worst case scenario" with
only minor performance degradation even if most of the time the arithmetic
could in fact be done with a narrower type. Also note that unsigned
fixed precision types small enough to fit inside the largest native
integer become a simple wrapper around that type, this includes the
"checked" variants. Small signed types will always have an
extra sign word and so be larger than their native equivalent.
-
When used at fixed precision and MaxBits is smaller than the number
of bits in the largest native integer type, then internally
cpp_int_backend switches to a "trivial"
implementation where it is just a thin wrapper around a single integer.
Note that it will still be slightly slower than a bare native integer,
as it emulates a signed-magnitude representation rather than simply
using the platforms native sign representation: this ensures there
is no step change in behavior as a cpp_int grows in size.
-
Fixed precision
cpp_int's
have some support for constexpr
values and user-defined literals, see here
for the full description. For example 0xfffff_cppi1024 specifies a 1024-bit integer
with the value 0xffff. This can be used to generate compile time constants
that are too large to fit into any built in number type.
-
You can import/export the raw bits of a cpp_int
to and from external storage via the
import_bits
and export_bits functions.
More information is in the section
on import/export.
#include <boost/multiprecision/cpp_int.hpp>
#include <iostream>
int main()
{
using namespace boost::multiprecision;
int128_t v = 1;
for(unsigned i = 1; i <= 20; ++i)
v *= i;
std::cout << v << std::endl;
cpp_int u = 1;
for(unsigned i = 1; i <= 100; ++i)
u *= i;
std::cout << u << std::endl;
return 0;
}
 Boost
C++ Libraries
Boost
C++ Libraries