 Boost
C++ Libraries
Boost
C++ Libraries
...one of the most highly
regarded and expertly designed C++ library projects in the
world.
— Herb Sutter and Andrei
Alexandrescu, C++
Coding Standards
 Boost
C++ Libraries
Boost
C++ Libraries
...one of the most highly
regarded and expertly designed C++ library projects in the
world.
— Herb Sutter and Andrei
Alexandrescu, C++
Coding Standards
The Remez algorithm is a methodology for locating the minimax rational approximation to a function. This short article gives a brief overview of the method, but it should not be regarded as a thorough theoretical treatment, for that you should consult your favorite textbook.
Imagine that you want to approximate some function f(x) by way of a rational function R(x), where R(x) may be either a polynomial P(x) or a ratio of two polynomials P(x)/Q(x) (a rational function). Initially we'll concentrate on the polynomial case, as it's by far the easier to deal with, later we'll extend to the full rational function case.
We want to find the "best" rational approximation, where "best" is defined to be the approximation that has the least deviation from f(x). We can measure the deviation by way of an error function:
Eabs(x) = f(x) - R(x)
which is expressed in terms of absolute error, but we can equally use relative error:
Erel(x) = (f(x) - R(x)) / |f(x)|
And indeed in general we can scale the error function in any way we want, it makes no difference to the maths, although the two forms above cover almost every practical case that you're likely to encounter.
The minimax rational function R(x) is then defined to be the function that yields the smallest maximal value of the error function. Chebyshev showed that there is a unique minimax solution for R(x) that has the following properties:
That means that if we know the location of the extrema of the error function then we can write N+2 simultaneous equations:
R(xi) + (-1)iE = f(xi)
where E is the maximal error term, and xi are the abscissa values of the N+2 extrema of the error function. It is then trivial to solve the simultaneous equations to obtain the polynomial coefficients and the error term.
Unfortunately we don't know where the extrema of the error function are located!
The Remez method is an iterative technique which, given a broad range of assumptions, will converge on the extrema of the error function, and therefore the minimax solution.
In the following discussion we'll use a concrete example to illustrate the Remez method: an approximation to the function ex over the range [-1, 1].
Before we can begin the Remez method, we must obtain an initial value for the location of the extrema of the error function. We could "guess" these, but a much closer first approximation can be obtained by first constructing an interpolated polynomial approximation to f(x).
In order to obtain the N+1 coefficients of the interpolated polynomial we need N+1 points (x0...xN): with our interpolated form passing through each of those points that yields N+1 simultaneous equations:
f(xi) = P(xi) = c0 + c1xi ... + cNxiN
Which can be solved for the coefficients c0...cN in P(x).
Obviously this is not a minimax solution, indeed our only guarantee is that f(x) and P(x) touch at N+1 locations, away from those points the error may be arbitrarily large. However, we would clearly like this initial approximation to be as close to f(x) as possible, and it turns out that using the zeros of an orthogonal polynomial as the initial interpolation points is a good choice. In our example we'll use the zeros of a Chebyshev polynomial as these are particularly easy to calculate, interpolating for a polynomial of degree 4, and measuring relative error we get the following error function:
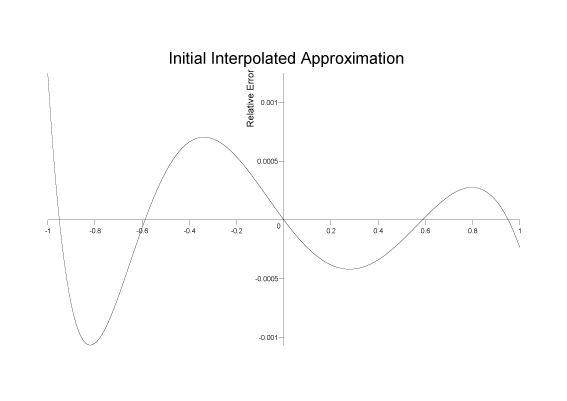
Which has a peak relative error of 1.2x10-3.
While this is a pretty good approximation already, judging by the shape of the error function we can clearly do better. Before starting on the Remez method propper, we have one more step to perform: locate all the extrema of the error function, and store these locations as our initial Chebyshev control points.
![[Note]](../../../../../../../doc/html/images/note.png) |
Note |
|---|---|
|
In the simple case of a polynomial approximation, by interpolating through the roots of a Chebyshev polynomial we have in fact created a Chebyshev approximation to the function: in terms of absolute error this is the best a priori choice for the interpolated form we can achieve, and typically is very close to the minimax solution. However, if we want to optimise for relative error, or if the approximation is a rational function, then the initial Chebyshev solution can be quite far from the ideal minimax solution. A more technical discussion of the theory involved can be found in this online course. |
The first step in the Remez method, given our current set of N+2 Chebyshev control points xi, is to solve the N+2 simultaneous equations:
P(xi) + (-1)iE = f(xi)
To obtain the error term E, and the coefficients of the polynomial P(x).
This gives us a new approximation to f(x) that has the same error E at each of the control points, and whose error function alternates in sign at the control points. This is still not necessarily the minimax solution though: since the control points may not be at the extrema of the error function. After this first step here's what our approximation's error function looks like:
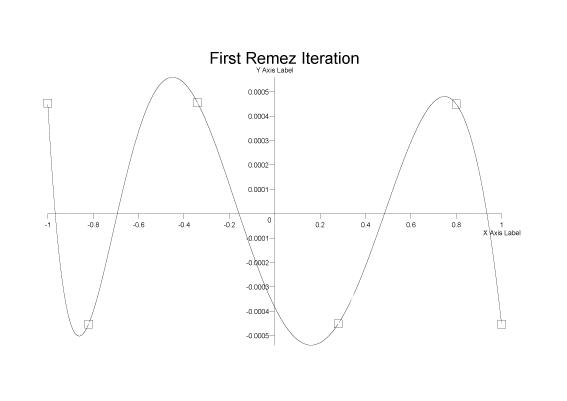
Clearly this is still not the minimax solution since the control points are not located at the extrema, but the maximum relative error has now dropped to 5.6x10-4.
The second step is to locate the extrema of the new approximation, which we do in two stages: first, since the error function changes sign at each control point, we must have N+1 roots of the error function located between each pair of N+2 control points. Once these roots are found by standard root finding techniques, we know that N extrema are bracketed between each pair of roots, plus two more between the endpoints of the range and the first and last roots. The N+2 extrema can then be found using standard function minimisation techniques.
We now have a choice: multi-point exchange, or single point exchange.
In single point exchange, we move the control point nearest to the largest extrema to the absissa value of the extrema.
In multi-point exchange we swap all the current control points, for the locations of the extrema.
In our example we perform multi-point exchange.
The Remez method then performs steps 1 and 2 above iteratively until the control points are located at the extrema of the error function: this is then the minimax solution.
For our current example, two more iterations converges on a minimax solution with a peak relative error of 5x10-4 and an error function that looks like:
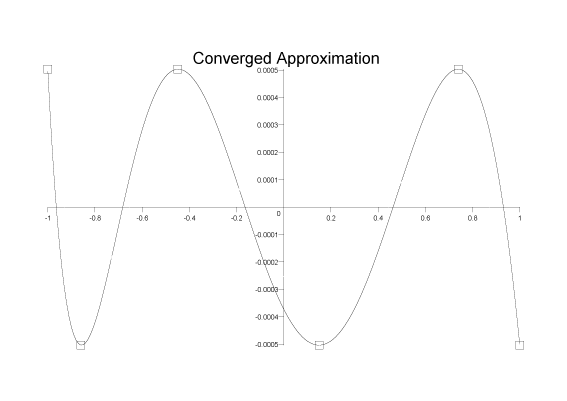
If we wish to extend the Remez method to a rational approximation of the form
f(x) = R(x) = P(x) / Q(x)
where P(x) and Q(x) are polynomials, then we proceed as before, except that now we have N+M+2 unknowns if P(x) is of order N and Q(x) is of order M. This assumes that Q(x) is normalised so that it's leading coefficient is 1, giving N+M+1 polynomial coefficients in total, plus the error term E.
The simultaneous equations to be solved are now:
P(xi) / Q(xi) + (-1)iE = f(xi)
Evaluated at the N+M+2 control points xi.
Unfortunately these equations are non-linear in the error term E: we can only solve them if we know E, and yet E is one of the unknowns!
The method usually adopted to solve these equations is an iterative one: we guess the value of E, solve the equations to obtain a new value for E (as well as the polynomial coefficients), then use the new value of E as the next guess. The method is repeated until E converges on a stable value.
These complications extend the running time required for the development of rational approximations quite considerably. It is often desirable to obtain a rational rather than polynomial approximation none the less: rational approximations will often match more difficult to approximate functions, to greater accuracy, and with greater efficiency, than their polynomial alternatives. For example, if we takes our previous example of an approximation to ex, we obtained 5x10-4 accuracy with an order 4 polynomial. If we move two of the unknowns into the denominator to give a pair of order 2 polynomials, and re-minimise, then the peak relative error drops to 8.7x10-5. That's a 5 fold increase in accuracy, for the same number of terms overall.
Most treatises on approximation theory stop at this point. However, from a practical point of view, most of the work involves finding the right approximating form, and then persuading the Remez method to converge on a solution.
So far we have used a direct approximation:
f(x) = R(x)
But this will converge to a useful approximation only if f(x) is smooth. In addition round-off errors when evaluating the rational form mean that this will never get closer than within a few epsilon of machine precision. Therefore this form of direct approximation is often reserved for situations where we want efficiency, rather than accuracy.
The first step in improving the situation is generally to split f(x) into a dominant part that we can compute accurately by another method, and a slowly changing remainder which can be approximated by a rational approximation. We might be tempted to write:
f(x) = g(x) + R(x)
where g(x) is the dominant part of f(x), but if f(x)/g(x) is approximately constant over the interval of interest then:
f(x) = g(x)(c + R(x))
Will yield a much better solution: here c is a constant that is the approximate value of f(x)/g(x) and R(x) is typically tiny compared to c. In this situation if R(x) is optimised for absolute error, then as long as its error is small compared to the constant c, that error will effectively get wiped out when R(x) is added to c.
The difficult part is obviously finding the right g(x) to extract from your function: often the asymptotic behaviour of the function will give a clue, so for example the function erfc becomes proportional to e-x2/x as x becomes large. Therefore using:
erfc(z) = (C + R(x)) e-x2/x
as the approximating form seems like an obvious thing to try, and does indeed yield a useful approximation.
However, the difficulty then becomes one of converging the minimax solution. Unfortunately, it is known that for some functions the Remez method can lead to divergent behaviour, even when the initial starting approximation is quite good. Furthermore, it is not uncommon for the solution obtained in the first Remez step above to be a bad one: the equations to be solved are generally "stiff", often very close to being singular, and assuming a solution is found at all, round-off errors and a rapidly changing error function, can lead to a situation where the error function does not in fact change sign at each control point as required. If this occurs, it is fatal to the Remez method. It is also possible to obtain solutions that are perfectly valid mathematically, but which are quite useless computationally: either because there is an unavoidable amount of roundoff error in the computation of the rational function, or because the denominator has one or more roots over the interval of the approximation. In the latter case while the approximation may have the correct limiting value at the roots, the approximation is nonetheless useless.
Assuming that the approximation does not have any fatal errors, and that the only issue is converging adequately on the minimax solution, the aim is to get as close as possible to the minimax solution before beginning the Remez method. Using the zeros of a Chebyshev polynomial for the initial interpolation is a good start, but may not be ideal when dealing with relative errors and/or rational (rather than polynomial) approximations. One approach is to skew the initial interpolation points to one end: for example if we raise the roots of the Chebyshev polynomial to a positive power greater than 1 then the roots will be skewed towards the middle of the [-1,1] interval, while a positive power less than one will skew them towards either end. More usefully, if we initially rescale the points over [0,1] and then raise to a positive power, we can skew them to the left or right. Returning to our example of ex over [-1,1], the initial interpolated form was some way from the minimax solution:

However, if we first skew the interpolation points to the left (rescale them to [0, 1], raise to the power 1.3, and then rescale back to [-1,1]) we reduce the error from 1.3x10-3to 6x10-4:
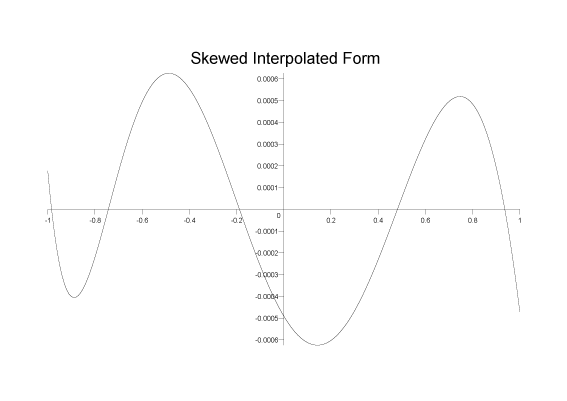
It's clearly still not ideal, but it is only a few percent away from our desired minimax solution (5x10-4).
The following lists some of the things to check if the Remez method goes wrong, it is by no means an exhaustive list, but is provided in the hopes that it will prove useful.
The original references for the Remez Method and it's extension to rational functions are unfortunately in Russian:
Remez, E.Ya., Fundamentals of numerical methods for Chebyshev approximations, "Naukova Dumka", Kiev, 1969.
Remez, E.Ya., Gavrilyuk, V.T., Computer development of certain approaches to the approximate construction of solutions of Chebyshev problems nonlinearly depending on parameters, Ukr. Mat. Zh. 12 (1960), 324-338.
Gavrilyuk, V.T., Generalization of the first polynomial algorithm of E.Ya.Remez for the problem of constructing rational-fractional Chebyshev approximations, Ukr. Mat. Zh. 16 (1961), 575-585.
Some English language sources include:
Fraser, W., Hart, J.F., On the computation of rational approximations to continuous functions, Comm. of the ACM 5 (1962), 401-403, 414.
Ralston, A., Rational Chebyshev approximation by Remes' algorithms, Numer.Math. 7 (1965), no. 4, 322-330.
A. Ralston, Rational Chebyshev approximation, Mathematical Methods for Digital Computers v. 2 (Ralston A., Wilf H., eds.), Wiley, New York, 1967, pp. 264-284.
Hart, J.F. e.a., Computer approximations, Wiley, New York a.o., 1968.
Cody, W.J., Fraser, W., Hart, J.F., Rational Chebyshev approximation using linear equations, Numer.Math. 12 (1968), 242-251.
Cody, W.J., A survey of practical rational and polynomial approximation of functions, SIAM Review 12 (1970), no. 3, 400-423.
Barrar, R.B., Loeb, H.J., On the Remez algorithm for non-linear families, Numer.Math. 15 (1970), 382-391.
Dunham, Ch.B., Convergence of the Fraser-Hart algorithm for rational Chebyshev approximation, Math. Comp. 29 (1975), no. 132, 1078-1082.
G. L. Litvinov, Approximate construction of rational approximations and the effect of error autocorrection, Russian Journal of Mathematical Physics, vol.1, No. 3, 1994.