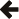#include <boost/multiprecision/cpp_dec_float.hpp>
namespace boost{ namespace multiprecision{
template <unsigned Digits10, class ExponentType = boost::int32_t, class Allocator = void>
class cpp_dec_float;
typedef number<cpp_dec_float<50> > cpp_dec_float_50;
typedef number<cpp_dec_float<100> > cpp_dec_float_100;
}}
The cpp_dec_float back-end
is used in conjunction with number:
It acts as an entirely C++ (header only and dependency free) floating-point
number type that is a drop-in replacement for the native C++ floating-point
types, but with much greater precision.
Type cpp_dec_float can
be used at fixed precision by specifying a non-zero Digits10
template parameter. The typedefs cpp_dec_float_50
and cpp_dec_float_100 provide
arithmetic types at 50 and 100 decimal digits precision respectively. Optionally,
you can specify an integer type to use for the exponent, this defaults
to a 32-bit integer type which is more than large enough for the vast majority
of use cases, but larger types such as long
long can also be specified if you
need a truly huge exponent range. In any case the ExponentType must be
a built in signed integer type at least 2 bytes and 16-bits wide.
Normally cpp_dec_float
allocates no memory: all of the space required for its digits are allocated
directly within the class. As a result care should be taken not to use
the class with too high a digit count as stack space requirements can grow
out of control. If that represents a problem then providing an allocator
as the final template parameter causes cpp_dec_float
to dynamically allocate the memory it needs: this significantly reduces
the size of cpp_dec_float
and increases the viable upper limit on the number of digits at the expense
of performance. However, please bear in mind that arithmetic operations
rapidly become very expensive as the digit count grows:
the current implementation really isn't optimized or designed for large
digit counts.
There is full standard library and numeric_limits
support available for this type.
Things you should know when using this type:
-
Default constructed
cpp_dec_floats
have a value of zero.
-
The radix of this type is 10. As a result it can behave subtly differently
from base-2 types.
-
The type has a number of internal guard digits over and above those
specified in the template argument. Normally these should not be visible
to the user.
-
The type supports both infinities and NaN's. An infinity is generated
whenever the result would overflow, and a NaN is generated for any
mathematically undefined operation.
-
There is a
std::numeric_limits specialisation for
this type.
-
Any
number instantiated
on this type, is convertible to any other number
instantiated on this type - for example you can convert from number<cpp_dec_float<50> > to number<cpp_dec_float<SomeOtherValue> >.
Narrowing conversions are truncating and explicit.
-
Conversion from a string results in a
std::runtime_error
being thrown if the string can not be interpreted as a valid floating
point number.
-
The actual precision of a
cpp_dec_float
is always slightly higher than the number of digits specified in the
template parameter, actually how much higher is an implementation detail
but is always at least 8 decimal digits.
-
Operations involving
cpp_dec_float
are always truncating. However, note that since their are guard digits
in effect, in practice this has no real impact on accuracy for most
use cases.
#include <boost/multiprecision/cpp_dec_float.hpp>
using namespace boost::multiprecision;
cpp_dec_float_100 b = 2;
std::cout << std::numeric_limits<cpp_dec_float_100>::digits << std::endl;
std::cout << std::numeric_limits<cpp_dec_float_100>::digits10 << std::endl;
std::cout << std::setprecision(std::numeric_limits<cpp_dec_float_100>::max_digits10)
<< log(b) << std::endl;
std::cout << boost::math::tgamma(b) << std::endl;
std::cout << boost::math::tgamma(b * b) << std::endl;
std::cout << boost::math::tgamma(cpp_dec_float_100(1000)) << std::endl;
 Boost
C++ Libraries
Boost
C++ Libraries