 Boost
C++ Libraries
Boost
C++ Libraries
...one of the most highly
regarded and expertly designed C++ library projects in the
world.
— Herb Sutter and Andrei
Alexandrescu, C++
Coding Standards
 Boost
C++ Libraries
Boost
C++ Libraries
...one of the most highly
regarded and expertly designed C++ library projects in the
world.
— Herb Sutter and Andrei
Alexandrescu, C++
Coding Standards
#include <boost/math/distributions/non_central_f.hpp>
namespace boost{ namespace math{ template <class RealType = double, class Policy = policies::policy<> > class non_central_f_distribution; typedef non_central_f_distribution<> non_central_f; template <class RealType, class Policy> class non_central_f_distribution { public: typedef RealType value_type; typedef Policy policy_type; // Constructor: non_central_f_distribution(RealType v1, RealType v2, RealType lambda); // Accessor to degrees_of_freedom parameters v1 & v2: RealType degrees_of_freedom1()const; RealType degrees_of_freedom2()const; // Accessor to non-centrality parameter lambda: RealType non_centrality()const; }; }} // namespaces
The noncentral F distribution is a generalization of the Fisher F Distribution. It is defined as the ratio
F = (X/v1) / (Y/v2)
where X is a noncentral χ2 random variable with v1 degrees of freedom and non-centrality parameter λ, and Y is a central χ2 random variable with v2 degrees of freedom.
This gives the following PDF:

where Lab(c) is a generalised Laguerre polynomial and B(a,b) is the beta function, or
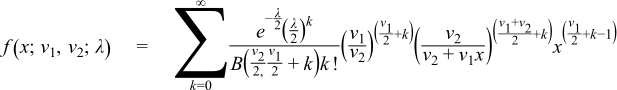
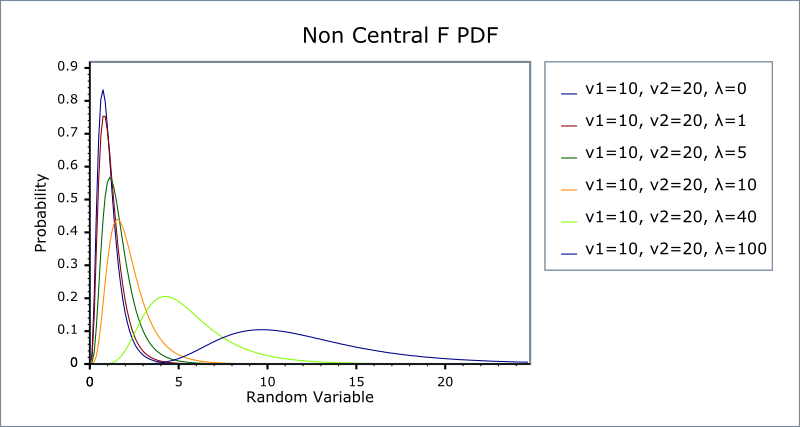
The following graph illustrates how the distribution changes for different values of λ:
non_central_f_distribution(RealType v1, RealType v2, RealType lambda);
Constructs a non-central beta distribution with parameters v1 and v2 and non-centrality parameter lambda.
Requires v1 > 0, v2 > 0 and lambda >= 0, otherwise calls domain_error.
RealType degrees_of_freedom1()const;
Returns the parameter v1 from which this object was constructed.
RealType degrees_of_freedom2()const;
Returns the parameter v2 from which this object was constructed.
RealType non_centrality()const;
Returns the non-centrality parameter lambda from which this object was constructed.
All the usual non-member accessor functions that are generic to all distributions are supported: Cumulative Distribution Function, Probability Density Function, Quantile, Hazard Function, Cumulative Hazard Function, mean, median, mode, variance, standard deviation, skewness, kurtosis, kurtosis_excess, range and support.
The domain of the random variable is [0, +∞].
This distribution is implemented in terms of the Noncentral Beta Distribution: refer to that distribution for accuracy data.
Since this distribution is implemented by adapting another distribution, the tests consist of basic sanity checks computed by the R-2.5.1 Math library statistical package and its pbeta and dbeta functions.
In the following table v1 and v2 are the first and second degrees of freedom parameters of the distribution, λ is the non-centrality parameter, x is the random variate, p is the probability, and q = 1-p.
|
Function |
Implementation Notes |
|---|---|
|
|
Implemented in terms of the non-central beta PDF using the relation: f(x;v1,v2;λ) = (v1/v2) / ((1+y)*(1+y)) * g(y/(1+y);v1/2,v2/2;λ) where g(x; a, b; λ) is the non central beta PDF, and: y = x * v1 / v2 |
|
cdf |
Using the relation: p = By(v1/2, v2/2; λ) where Bx(a, b; λ) is the noncentral beta distribution CDF and y = x * v1 / v2 |
|
cdf complement |
Using the relation: q = 1 - By(v1/2, v2/2; λ) where 1 - Bx(a, b; λ) is the complement of the noncentral beta distribution CDF and y = x * v1 / v2 |
|
quantile |
Using the relation: x = (bx / (1-bx)) * (v1 / v2) where bx = Qp-1(v1/2, v2/2; λ) and Qp-1(v1/2, v2/2; λ) is the noncentral beta quantile. |
|
quantile from the complement |
Using the relation: x = (bx / (1-bx)) * (v1 / v2) where bx = QCq-1(v1/2, v2/2; λ) and QCq-1(v1/2, v2/2; λ) is the noncentral beta quantile from the complement. |
|
mean |
v2 * (v1 + l) / (v1 * (v2 - 2)) |
|
mode |
By numeric maximalisation of the PDF. |
|
variance |
Refer to, Weisstein, Eric W. "Noncentral F-Distribution." From MathWorld--A Wolfram Web Resource. |
|
skewness |
Refer to, Weisstein, Eric W. "Noncentral F-Distribution." From MathWorld--A Wolfram Web Resource., and to the Mathematica documentation |
|
kurtosis and kurtosis excess |
Refer to, Weisstein, Eric W. "Noncentral F-Distribution." From MathWorld--A Wolfram Web Resource., and to the Mathematica documentation |
Some analytic properties of noncentral distributions (particularly unimodality, and monotonicity of their modes) are surveyed and summarized by:
Andrea van Aubel & Wolfgang Gawronski, Applied Mathematics and Computation, 141 (2003) 3-12.